德优网2020陕西省西安市未央区西安中学高中数学考试期末高一上
2019-2020学年陕西省西安中学高一（上）期末数学试卷
试卷总分:120分
命题人:dygzsxyn
考试时长:120分钟
一、选择题(12小题共48分)
1.
（本题4分）
下列函数中，既是偶函数又在区间（﹣∞，0）上单调递增的是（ ）
A.f（x）＝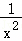
B.f（x）＝x2+1
C.f（x）＝x3
D.f（x）＝2﹣x
2.
（本题4分）
若函数y＝ax+b﹣1（a＞0且a≠1）的图象经过二、三、四象限，一定有（ ）
A.0＜a＜1且b＜0
B.．a＞1且b＞0
C.．0＜a＜1且b＞0
D.a＞1且b＜0
3.
（本题4分）
如图正方形OABC的边长为1，它是水平放置的一个平面图形的直观图，则原图形的面积（ ）
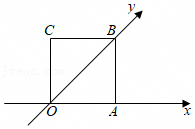
4.
（本题4分）
设a＝log73，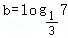
，c＝30.7，则a，b，c的大小关系是（ ）
A.．a＜b＜c
B.c＜b＜a
C.b＜c＜a
D.．b＜a＜c
5.
（本题4分）
如图所示，在四面体中，若直线EF和GH相交，则它们的交点一定（ ）
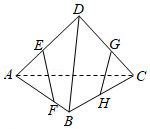
A.．在直线DB上
B.．在直线AB上
C.．在直线CB上
D.．都不对
6.
（本题4分）
在下列区间中，函数f（x）＝ex+4x﹣3的零点所在的区间为（ ）
A.（﹣2，﹣1）
B.（﹣1，0）
C.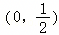
D.．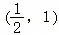
7.
（本题4分）
某四面体的三视图如图所示，正视图、俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大的为（ ）
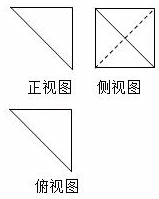
8.
（本题4分）
已知两个不同的平面α、β和两条不重合的直线m、n，有下列四个命题：
①若m∥n，m⊥α，则n⊥α；
②若m⊥α，m⊥β，则α∥β；
③若m⊥α，m∥n，n⊂β，则α⊥β；
④若m∥α，α∩β＝n，则m∥n
其中正确命题的个数是（ ）
9.
（本题4分）
若不等式x2﹣2ax+a＞0对一切实数R恒成立，则关于t的不等式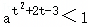
的解集为（ ）
|
A.（﹣3，1）
|
B.（﹣∞，﹣3）∪（1，+∞）
|
|
C.∅
|
D.（0，1）
|
10.
（本题4分）
已知f（x）＝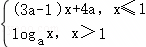
是（﹣∞，+∞）上的减函数，那么a的取值范围是（ ）
11.
（本题4分）
已知奇函数f（x）在x≥0时的图象如图所示，则不等式xf（x）＜0的解集为（ ）
|
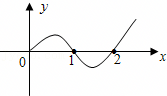
A.（1，2）
|
B.．（﹣2，﹣1）
|
|
C.．（﹣2，﹣1）∪（1，2）
|
D.（﹣1，1）
|
12.
（本题4分）
根据有关资料，围棋状态空间复杂度的上限M约为3361，而可观测宇宙中普通物质的原子总数N约为1080，则下列各数中与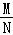
最接近的是（ ）
（参考数据：lg3≈0.48）
A.1033
B.1053
C.1073
D.．1093
二、填空题(4小题共16分)
13.
（本题4分）
若方程x2﹣2mx+4m＝0的两根满足一根大于0，一根小于0，则m的取值范围是 ．
14.
（本题4分）
已知函数y＝f（x）的图象关于原点对称，当x＜0时，f（x）＝x（1﹣x），则当x＞0时，函数f（x）＝ ．
15.
（本题4分）
已知各顶点都在一个球面上的正四棱柱（底面为正方形，侧棱与底面垂直的棱柱）高为4，体积为16，则这个球的表面积是 ．（参考公式：球的表面积S＝4πR2）
16.
（本题4分）
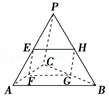
正三棱锥P﹣ABC的底面边长为1，E，F，G，H分别是PA，AC，BC，PB的中点，四边形EFGH的面积为S，则S的取值范围是 ．
三、解答题(6小题共56分)
17.
（本题8分）
求满足下列条件的直线的一般式方程：
（1）经过点A（﹣1，2），且与x轴垂直；
（2）经过两点A（﹣3，5），B（4，﹣2）．
18.
（本题8分）
已知集合A＝{x|m﹣1≤x≤2m+3}，B＝{x|lg（﹣x2+2x+9）＞0}．
（1）当m＝2时，求A∪B、（∁RA）∩B；
（2）若A∩B＝A，求实数m的取值范围．
19.
（本题10分）
已知函数f（x）＝loga（1﹣x）+loga（x+3）（0＜a＜1）．
（Ⅰ）求函数f（x）的定义域；
（Ⅱ）若函数f（x）的最小值为﹣4，求实数a的值．
20.
（本题10分）
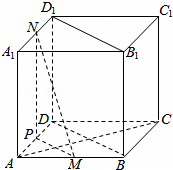
如图，在正方体ABCD﹣A1B1C1D1中，M，N，P分别是棱AB，A1D1，AD的中点，求证：
（Ⅰ）平面MNP∥平面BDD1B1；
（Ⅱ）MN⊥AC．
21.
（本题10分）
近年来，雾霾日趋严重，我们的工作、生活受到了严重的影响，如何改善空气质量已成为当今的热点问题．某空气净化器制造厂，决定投入生产某型号的空气净化器，根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产该型号空气净化器x（百台），其总成本为P（x）（万元），其中固定成本为12万元，并且每生产1百台的生产成本为10万元（总成本＝固定成本+生产成本）．销售收入Q（x）（万元）满足Q（x）＝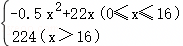
，假定该产品产销平衡（即生产的产品都能卖掉），根据以上统计规律，请完成下列问题：
（1）求利润函数y＝f（x）的解析式（利润＝销售收入﹣总成本）；
（2）工厂生产多少百台产品时，可使利润最多？
22.
（本题10分）
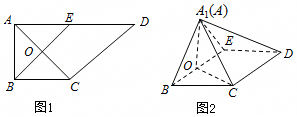
如图，在直角梯形ABCD中，AD∥BC，∠BAD＝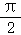
，AB＝BC＝
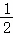AD＝a，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到如图2中△A1BE的位置，得到四棱锥A1﹣BCDE．
（Ⅰ）证明：CD⊥平面A1OC；
（Ⅱ）当平面A1BE⊥平面BCDE时，四棱锥A1﹣BCDE的体积为36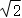
，求a的值．
转载声明：
本题解析属于发布者收集录入，如涉及版权请向平台申诉！
！版权申诉
解析
纠错
收藏
下载
相似
组卷
