首页 > 试卷详情

德优网2021陕西省西安市未央区西安中学高中数学模考模拟

2021年陕西省西安中学高考数学七模试卷（文科）

试卷总分:150分命题人:dygzsxyn 考试时长:120分钟

一、选择题(12小题共60分)

1. （本题5分）已知集合A＝{x|x²+x﹣2＞0}，B＝{﹣1，0，2}，则（∁_RA）∩B＝（　　）

A.{2}

B.{﹣1，0}

C.{0，2}

D.{﹣1，0，2}

解析

纠错

下载

相似

组卷

2. （本题5分）复数z满足z•（1+i）＝2i，则|z﹣2i|＝（　　）

A.．

B.．

解析

纠错

下载

相似

组卷

3. （本题5分）据《乾陵百迷》记载：乾陵是陕西关中地区唐十八陵之一，位于乾县县城北部的梁山上，是唐高宗李治和武则天的合葬墓．乾陵是目前保存最完好的一座帝王陵墓．1961年3月被国务院公布为第一批全国重点文物保护单位．乾陵气势雄伟，规模宏大．登乾陵需要通过一段石阶路，如图所示，石阶路共526级台阶（各台阶高度相同）和18座平台，宽11米，全路用32000块富平墨玉石砌成．右阶有许多象征意义．比如第一道平台的34级台阶，象征唐高宗李治在位执政34年，第二道平台的21级台阶，象征武则天执政21年，……，第九道平台的108级台阶，象征有108个“吉祥”．现已知这108级台阶落差高度为17.69米，那么乾陵石阶路526级台阶的落差高度约为（　　）

A.86.2米

B.．83.6米

C.．84.8米

D.．85.8米

解析

纠错

下载

相似

组卷

4. （本题5分）已知a＝

，b＝

，c＝

，则（　　）

A.．a＞b＞c

B.c＞b＞a

C.c＞a＞b

D.．a＞c＞b

解析

纠错

下载

相似

组卷

5. （本题5分）向量

＝（2，1），

＝（﹣3，4），

＝（3m﹣1，1﹣2m），若（

）⊥

，则实数m等于（　　）

A.1

D.．2

解析

纠错

下载

相似

组卷

6. （本题5分）在等比数列{a_n}中，a₁a₃＝a₄＝4，则a₆＝（　　）

A.．6

B.．±8

C.．﹣8

D.．8

解析

纠错

下载

相似

组卷

7. （本题5分）刘徽（约公元225年﹣295年），魏晋时期伟大的数学家，中国古典数学理论的奠基人之一．他在割圆术中提出的“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体，而无所失矣”，这可视为中国古代极限观念的佳作．割圆术的核心思想是将一个圆的内接正n边形等分成n个等腰三角形（如图所示），当n变得很大时，这n个等腰三角形的面积之和近似等于圆的面积．运用割圆术的思想，估计sin4°的值为（　　）

A.0.0524

B.．0.0628

C.0.0785

D.．0.0698

解析

纠错

下载

相似

组卷

8. （本题5分）设直线x﹣y﹣a＝0与圆x²+y²＝4相交于A，B两点，O为坐标原点，若△AOB为等边三角形，则实数a的值为（　　）

C.±3

D.．±9

解析

纠错

下载

相似

组卷

9. （本题5分）执行如图所示的程序框图，则输出的a值为（　　）

B.﹣3

D.．2

解析

纠错

下载

相似

组卷

10. （本题5分）已知函数

，则（　　）

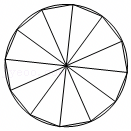
A.f（x）在（0，4）单调递减

B.f（x）在（0，2）单调递减，在（2，4）单调递增

C.．y＝f（x）的图象关于点（2，0）对称

D.y＝f（x）的图象关于直线x＝2对称

解析

纠错

下载

相似

组卷

11. （本题5分）如图，从双曲线

的左焦点F引圆x²+y²＝a²的切线，切点为T，延长FT交双曲线右支于P点，若M为线段FP的中点，O为坐标原点，则|MO|﹣|MT|与b﹣a的大小关系为（　　）

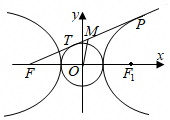
A.．\|MO\|﹣\|MT\|＞b﹣a	B.．\|MO\|﹣\|MT\|＜b﹣a
C.．\|MO\|﹣\|MT\|＝b﹣a	D.以上三种可能都有

解析

纠错

下载

相似

组卷

12. （本题5分）高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的美誉，用其名字命名的“高斯函数”：设x∈R，用[x]表示不超过x的最大整数，则y＝[x]称为高斯函数，也称取整函数，例如：[﹣3.7]＝﹣4，[2.3]＝2．已知f（x）＝

，则函数y＝[f（x）]的值域为（　　）

A.{0}

B.．{﹣1，0}

C.．{﹣2，﹣1，0}

D.．{﹣1，0，1}

解析

纠错

下载

相似

组卷

二、填空题(4小题共20分)

13. （本题5分）设等差数列{a_n}的前n项和为S_n，若a₂+a₄+a₉＝24，则S₉＝　．

解析

纠错

下载

相似

组卷

14. （本题5分）曲线y＝lnx﹣

在x＝1处的切线的倾斜角为α，则sin（α+

）＝　．

解析

纠错

下载

相似

组卷

15. （本题5分）设实数x，y满足约束条件

，则z＝3x﹣y的最大值是　　．

解析

纠错

下载

相似

组卷

16. （本题5分）已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA＝AC，SB＝BC，三棱锥S﹣ABC的体积为9，则球O的表面积为　　．

解析

纠错

下载

相似

组卷

三、解答题(7小题共70分)

17. （本题12分）在△ABC中，内角A，B，C的对边分别为a，b，c，已知b＝acosC+

．
（1）求角A；
（2）若

＝3，求a的最小值．

解析

纠错

下载

相似

组卷

18. （本题12分）甲，乙两台机床同时生产一种零件，其质量按测试指标划分：指标大于或等于100为优品，大于等于90且小于100为合格品，小于90为次品，现随机抽取这两台车床生产的零件各100件进行检测，检测结果统计如下：

测试指标	[85，90）	[90，95）	[95，100）	[100，105）	[105，110）
机床甲	8	12	40	32	8
机床乙	7	18	40	29	6

（1）试分别估计甲机床、乙机床生产的零件为优品的概率；
（2）甲机床生产一件零件，若是优品可盈利160元，合格品可盈利100元，次品则亏损20元；假设甲机床某天生产50件零件，请估计甲机床该天的日利润（单位：元）；
（3）从甲、乙机床生产的零件指标在[90，95）内的零件中，采用分层抽样的方法抽取5件，从这5件中任选2件进行质量分析，求这2件都是乙机床生产的概率．

解析

纠错

下载

相似

组卷

19. （本题12分）如图，已知椭圆

的离心率为

，E的左顶点为A、上顶点为B，点P在椭圆上，且△PF₁F₂的周长为

．
（Ⅰ）求椭圆的方程；
（Ⅱ）设C，D是椭圆E上两不同点，CD∥AB，直线CD与x轴、y轴分别交于M，N两点，且

的取值范围．

解析

纠错

下载

相似

组卷

20. （本题12分）如图，在三棱锥P﹣ABC中，PA＝PB＝

，AC＝BC＝PC＝

，AB＝2，点D，E分别为AB，PC的中点．
（1）证明：PD⊥平面ABC；
（2）设点F在线段BC上，且

，若三棱锥P﹣AEF的体积为

，求实数λ的值．

解析

纠错

下载

相似

组卷

21. （本题12分）已知函数f（x）＝

．
（1）若函数f（x）的图象在x＝1处的切线为y＝1，求f（x）的极值；
（2）若f（x）≤e^x+

﹣1恒成立，求实数a的取值范围．

解析

纠错

下载

相似

组卷

22. （本题10分）在平面直角坐标系xOy中，曲线C₁的参数方程为

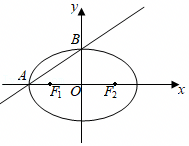
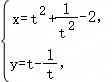（t为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C₂的极坐标方程为

．
（1）求曲线C₁的普通方程和C₂的直角坐标方程；
（2）设点P是曲线C₁与C₂的公共点，求圆心在极轴上，且经过极点和点P的圆的极坐标方程．

解析

纠错

下载

相似

组卷

23. （本题0分）已知函数f（x）＝|x﹣a|
（1）若f（x）≤m的解集为[﹣1，5]，求实数a，m的值
（2）当a＝2且0≤t＜2时，解关于x的不等式f（x）+t≥f（x+2）

解析

纠错

下载

相似

组卷

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

dygzsxyn

2021-06-06

高中数学 | 模考 | 难度:1.26

下载量
浏览量
收益额

同类试卷 更多>>

2021年陕西省西安市西安中学高考数学二模试卷（理科）

更新:2021-03-18 12:07浏览量:474

2024-2025学年陕西省西安市高新一中高三（上）月考数学试卷（二模）

更新:2024-03-18 04:53浏览量:12

2024-2025学年陕西省西安市高新一中高三（上）第三次模拟数学试卷

更新:2024-04-04 06:23浏览量:5

2024-2025学年陕西省西安建筑科技大学附属中学高三（上）月考数学试卷（一模）

更新:2024-03-13 08:20浏览量:10

2024-2025学年陕西省西安八十五中高三（上）第一次模拟数学试卷

更新:2024-03-12 06:30浏览量:4

2024-2025年陕西省西安市高新一中高三（上）第五次模拟数学试卷

更新:2024-05-13 09:53浏览量:6

2023-2024学年陕西省西安市周至四中高三（上）月考数学试卷（理科）（一模）

更新:2023-03-04 02:06浏览量:8

2024年陕西师大附中高考数学十模试卷（理科）

更新:2024-07-09 05:34浏览量:8

2024年陕西省西安中学高考数学模拟试卷（文科）（一）

更新:2024-03-07 08:48浏览量:6

2024年陕西省西安中学高考数学模拟试卷（理科）（一）

更新:2024-03-11 01:46浏览量:7

A.．\|MO\|﹣\|MT\|＞b﹣a	B.．\|MO\|﹣\|MT\|＜b﹣a
C.．\|MO\|﹣\|MT\|＝b﹣a	D.以上三种可能都有

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

普通登录

手机登录

微信扫码立即登录

2021年陕西省西安中学高考数学七模试卷（文科）