首页 > 试卷详情

德优网2023陕西省西安市碑林区西工大附中高中数学模考模拟

2023年陕西省西安市西工大附中高考数学第八次适应性试卷（理科）

试卷总分:150分命题人:dygzsxyn 考试时长:120分钟

一、选择题(12小题共60分)

1. （本题5分）已知集合A＝{x|ln（x+2）＞0}，集合B＝{x∈N|（x+1）（x﹣3）≤0}，则A∩B＝（　　）

A.{0，1，2，3}

B.{1，2，3}

C.{0，1，2，3，4}

D.{﹣1，0，1，2，3}

解析

纠错

下载

相似

组卷

2. （本题5分） “﹣2＜m＜2”是“x²﹣mx+1＞0在x∈（1，+∞）上恒成立”的（　　）

A.充分不必要条件	B.必要不充分条件
C.充要条件	D.．既不充分也不必要条件

解析

纠错

下载

相似

组卷

3. （本题5分）已知m，n是两条不重合的直线，α，β是两个不重合的平面，下列命题正确的是（　　）

A.．若m∥α，m∥β，n∥α，n∥β，则α∥β

B.若m∥n，m⊥α，n⊥β，则α∥β

C.．若m⊥n，m⊂α，n⊂β，则α⊥β

D.若m⊥n，m∥α，n⊥β，则α⊥β

解析

纠错

下载

相似

组卷

4. （本题5分）中国象牙雕刻中传统雕刻技艺的代表“象牙鬼工球”工艺被誉为是鬼斧神工．“鬼工球”又称“牙雕套球”，是通过高超的镂空技艺用整块象牙雕出层层象牙球，且每层象牙球可以自由转动，上面再雕有纹饰，是精美绝伦的中国国粹．据《格古要论》载，早在宋代就已出现三层套球，清代的时候就已经发展到十三层了．今一雕刻大师在棱长为6的整块正方体玉石内部套雕出一可以任意转动的球，在球内部又套雕出一个正四面体，若不计各层厚度和损失，最内层的正四面体棱最长为（　　）

B.．6

解析

纠错

下载

相似

组卷

5. （本题5分）已知平面向量

、

满足

，

，则

的最大值为（　　）

C.．

D.．2

解析

纠错

下载

相似

组卷

6. （本题5分）已知在△ABC中，角A，B，C的对边分别为a，b，c，且

，则能将△ABC全部覆盖的所有圆中，最小的圆的面积为（　　）

B.4π

C.．

D.．

解析

纠错

下载

相似

组卷

7. （本题5分）下列说法正确的有（　　）

A.已知一组数据7，7，8，9，5，6，8，8，则这组数据的中位数为8

B.已知一组数据x₁，x₂，x₃，…，x₁₀的方差为2，则x₁+2，x₂+2，x₃+2，…，x₁₀+2的方差为2

C.具有线性相关关系的变量x，y，其线性回归方程为＝0.2x﹣m，若样本点的中心为（m，3.2），则m＝4

D.若随机变量X服从正态分布N（2，σ²），P（X≤3）＝0.64，则P（1≤X≤2）＝0.14

解析

纠错

下载

相似

组卷

8. （本题5分） 1748年，瑞士数学家欧拉发现了复指数函数和三角函数的关系，并写出以下公式e^ix＝cosx+isinx（x∈R，i为虚数单位），这个公式在复变论中占有非常重要的地位，被誉为“数学中的天桥”．根据此公式，下面四个结果中不成立的是（　　）

A.eⁱ^π+1＝0	B.
C.\|e^ix+e^﹣ix\|≥2	D.．﹣2≤\|e^ix﹣e^﹣ix\|≤2

解析

纠错

下载

相似

组卷

9. （本题5分）若log₄（x+2y）+log₄（x﹣2y）＝1，则|x|﹣|y|的最小值是（　　）

A.．

B.．2

C.．

解析

纠错

下载

相似

组卷

10. （本题5分）已知数列{a_n}满足：a_n+a_n₊₂＝2a_n₊₁对n∈N^*恒成立，且

，其前n项和S_n有最大值，则使得S_n＞0的最大的n的值是（　　）

A.10

B.12

C.15

D.．17

解析

纠错

下载

相似

组卷

11. （本题5分）已知双曲线

的下、上焦点分别为F₁，F₂，点M在C的下支上，过点M作C的一条渐近线的垂线，垂足为D．若|MD|＞|F₁F₂|﹣|MF₂|恒成立，则C的离心率的取值范围为（　　）

B.．

C.（1，2）

D.．

解析

纠错

下载

相似

组卷

12. （本题5分）定义在R上的可导函数f（x）满足f（1）＝1，且2f'（x）＞1，当x∈[﹣

，

]时，不等式

的解集为（　　）

A.（

，

）

B.（﹣

，

）

C.（0，

）

D.．（﹣

，

）

解析

纠错

下载

相似

组卷

二、填空题(4小题共20分)

13. （本题5分）

的展开式中的常数项为　　．

解析

纠错

下载

相似

组卷

14. （本题5分）将8张连号的门票分给5个家庭，甲家庭需要3张连号的门票，乙家庭需要2张连号的门票，剩余的3张门票随机分给其余的3个家庭，并且甲乙两个家庭不能连排在一起（甲乙两个家庭内部成员的顺序不予考虑），则这8张门票不同的分配方法有　　种．

解析

纠错

下载

相似

组卷

15. （本题5分）已知函数f（x）＝sin（cosx）+cos（sinx）给出下列4个结论：
①f（x）是偶函数；
②f（x）在区间

上单调递减；
③f（x）的周期是π；
④f（x）的最大值为2；
其中正确的结论有　　．

解析

纠错

下载

相似

组卷

16. （本题5分）已知函数

在[﹣k，k]（k＞0）上的最大值与最小值分别为M和m，则函数g（x）＝（M+m）x+[（M+m）x﹣1]^﹣3的图象的对称中心是　．

解析

纠错

下载

相似

组卷

三、解答题(7小题共70分)

17. （本题12分）已知数列{a_n}满足a₁＝1，a₂＝3，数列{b_n}为等比数列，且满足b_n（a_n₊₁﹣a_n）＝b_n₊₁．
（1）求数列{a_n}的通项公式；
（2）数列{b_n}的前n项和为S_n，若 _____，记数列{c_n}满足c_n＝

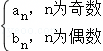，求数列{c_n}的前2n项和T_2n．
在①2S₂＝S₃﹣2；②b₂，2a₃，b₄成等差数列；③S₆＝126这三个条件中任选一个补充在第（2）问中，并对其求解．
注：若选择多个条件分别解答，按第一个解答计分．

解析

纠错

下载

相似

组卷

18. （本题12分）如图1，四边形ABCD为矩形，BC＝2AB，E为AD的中点，将△ABE、△DCE分别沿BE、CE折起得图2，使得平面ABE⊥平面BCE，平面DCE⊥平面BCE．
（Ⅰ）求证：平面ABE⊥平面DCE；
（Ⅱ）若F为线段BC的中点，求直线FA与平面ADE所成角的正弦值．

解析

纠错

下载

相似

组卷

19. （本题12分）某市为了传承发展中华优秀传统文化，组织该市中学生进行了一次文化知识有奖竞赛，竞赛奖励规则如下：得分在[70，80）内的学生获三等奖，得分在[80，90）内的学生获二等奖，得分在[90，100）内的学生获得一等奖，其他学生不得奖，为了解学生对相关知识的掌握情况，随机抽取100名学生的竞赛成绩，并以此为样本绘制了样本频率分布直方图，如图所示．
（1）现从该样本中随机抽取两名学生的竞赛成绩，求这两名学生中恰有一名学生获奖的概率；
（2）若该市所有参赛学生的成绩X近似服从正态分布N（μ，σ²），其中σ≈15，μ为样本平均数的估计值，利用所得正态分布模型解决以下问题：
（i）若该市共有10000名学生参加了竞赛，试估计参赛学生中成绩超过79分的学生数（结果四舍五入到整数）；
（ii）若从所有参赛学生中（参赛学生数大于10000）随机取3名学生进行访谈，设其中竞赛成绩在64分以上的学生数为ξ，求随机变量ξ的分布列和期望．
附参考数据，若随机变量X服从正态分布N（μ，σ²），则P（μ﹣σ≤X≤μ+σ）≈0.6827，P（μ﹣2σ≤X≤μ+2σ）≈0.9545，P（μ﹣3σ≤X≤μ+3σ）≈0.9973．

解析

纠错

下载

相似

组卷

20. （本题12分）如图，椭圆C₁：

＝1（a＞b＞0）的左右焦点分别为的F₁、F₂，离心率为

；过抛物线C₂：x²＝4by焦点F的直线交抛物线于M、N两点，当|MF|＝

时，M点在x轴上的射影为F₁．连结NO，MO并延长分别交C₁于A、B两点，连接AB；△OMN与△OAB的面积分别记为S_△OMN，S_△OAB，设λ＝

．
（Ⅰ）求椭圆C₁和抛物线C₂的方程；
（Ⅱ）求λ的取值范围．

解析

纠错

下载

相似

组卷

21. （本题12分）已知函数f（x）＝alnx﹣2x（a≠0）．
（1）讨论f（x）的单调性；
（2）当x＞0时，不等式

恒成立，求a的取值范围．

解析

纠错

下载

相似

组卷

22. （本题10分）在平面直角坐标系xOy中，曲线C的参数方程是

（φ为参数）．以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，已知直线l的极坐标方程为2ρcos（θ+

）﹣1＝0．
（1）求直线l的直角坐标方程和曲线C的普通方程；
（2）若直线l与x轴交于点P，与曲线C分别交于A，B两点，求|PA|•|PB|的值．

解析

纠错

下载

相似

组卷

23. （本题0分）．已知a＞0，b＞0，a+b＝1．
（1）求

的最大值；
（2）若不等式

对任意x∈R及条件中的任意a，b恒成立，求实数m的取值范围．

解析

纠错

下载

相似

组卷

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

dygzsxyn

2023-06-11

高中数学 | 模考 | 难度:1.61

下载量
浏览量
收益额

同类试卷 更多>>

2021年陕西省西安市西安中学高考数学二模试卷（理科）

更新:2021-03-18 12:07浏览量:473

2024-2025学年陕西省西安市高新一中高三（上）月考数学试卷（二模）

更新:2024-03-18 04:53浏览量:11

2024-2025学年陕西省西安市高新一中高三（上）第三次模拟数学试卷

更新:2024-04-04 06:23浏览量:5

2024-2025学年陕西省西安建筑科技大学附属中学高三（上）月考数学试卷（一模）

更新:2024-03-13 08:20浏览量:9

2024-2025学年陕西省西安八十五中高三（上）第一次模拟数学试卷

更新:2024-03-12 06:30浏览量:4

2024-2025年陕西省西安市高新一中高三（上）第五次模拟数学试卷

更新:2024-05-13 09:53浏览量:6

2023-2024学年陕西省西安市周至四中高三（上）月考数学试卷（理科）（一模）

更新:2023-03-04 02:06浏览量:7

2024年陕西师大附中高考数学十模试卷（理科）

更新:2024-07-09 05:34浏览量:8

2024年陕西省西安中学高考数学模拟试卷（文科）（一）

更新:2024-03-07 08:48浏览量:5

2024年陕西省西安中学高考数学模拟试卷（理科）（一）

更新:2024-03-11 01:46浏览量:6

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

普通登录

手机登录

微信扫码立即登录

2023年陕西省西安市西工大附中高考数学第八次适应性试卷（理科）