服务热线
搜题▪组卷
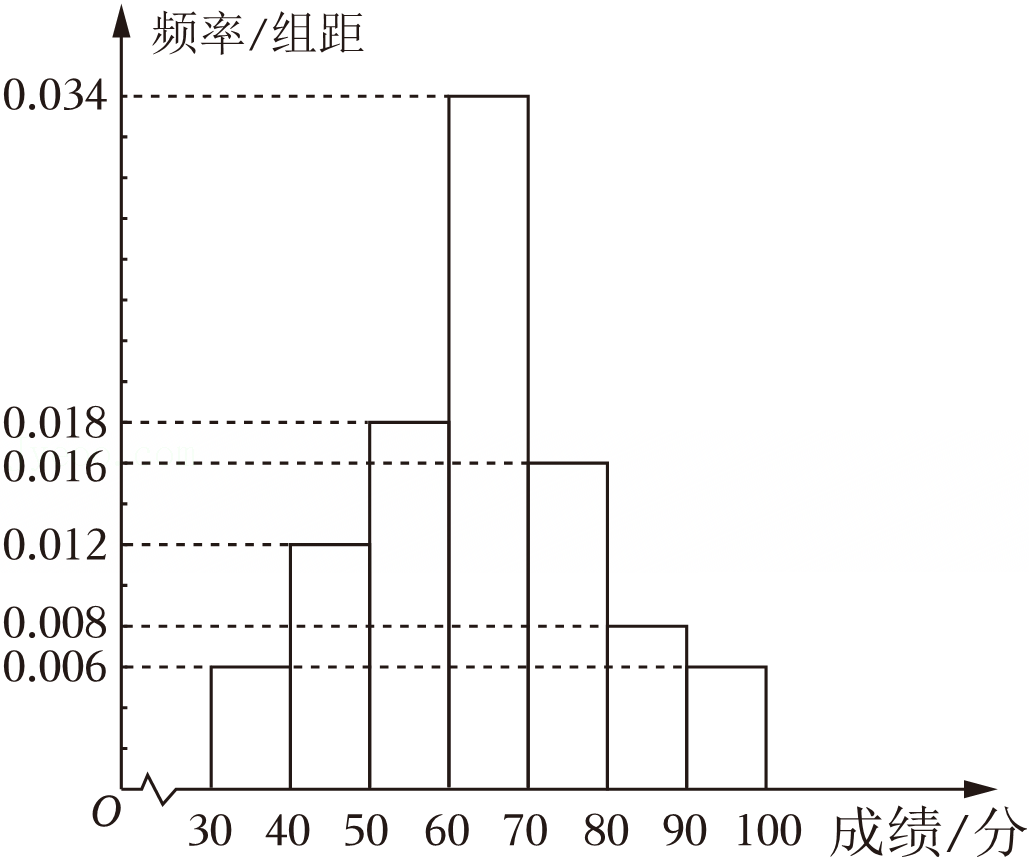
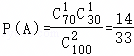 ,
,| ξ | 0 | 1 | 2 | 3 |
| P |
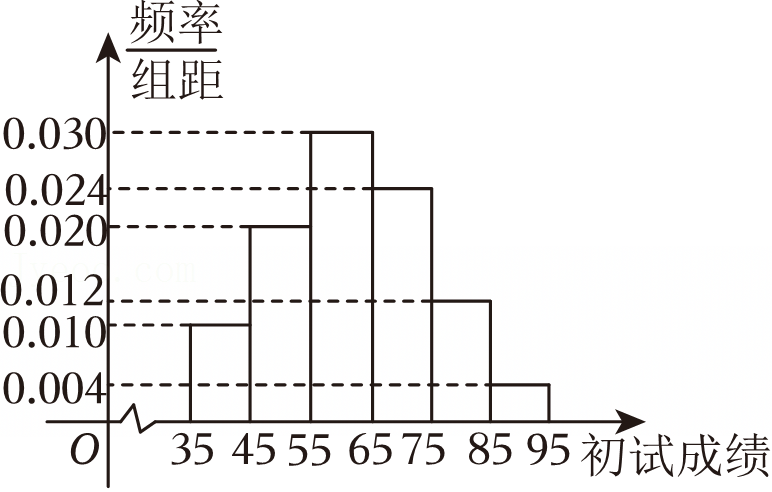
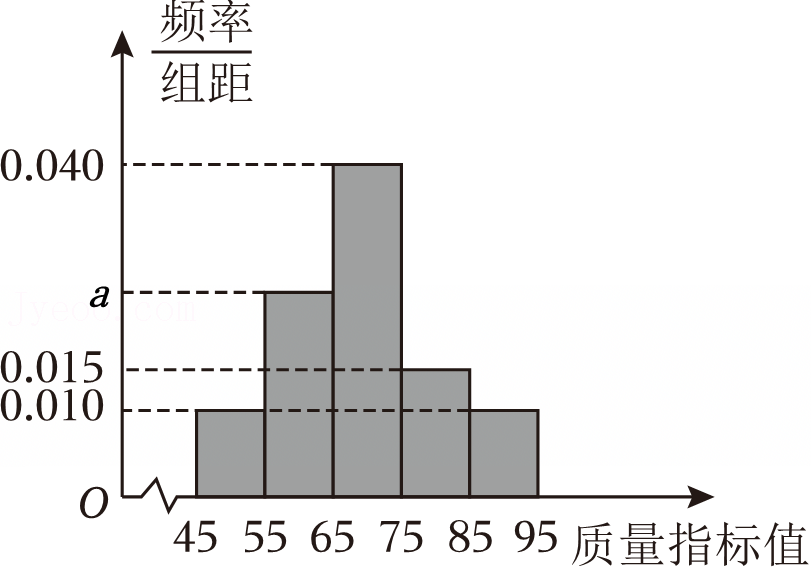
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 小于m | 不小于m | 合计 | |
| 朗读记忆(人数) | |||
| 默读记忆(人数) | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
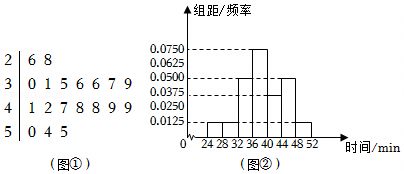
| 小于m | 不小于m | 合计 | |
| 朗读记忆(人数) | |||
| 默读记忆(人数) | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |

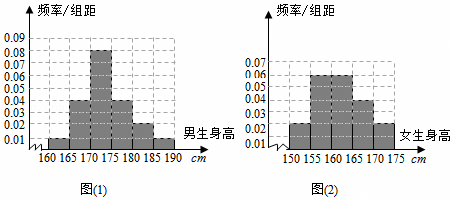
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
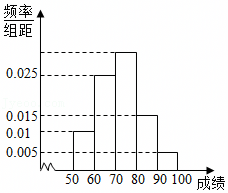

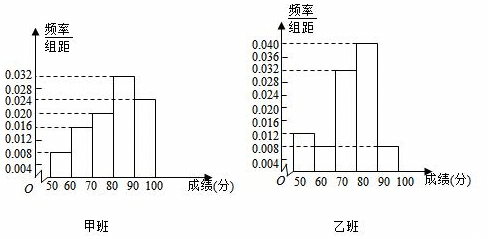
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
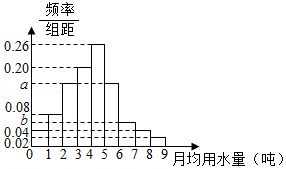
| 经常锻炼 | 不经常锻炼 | 合计 | |
| 合格 | 25 | ||
| 优秀 | 10 | ||
| 合计 | 100 |
| P(χ2≥5) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |

mnf@dyw.com
2023-06-11
高中数学 | | 解答题