首页 | 客服 | 上传赚现
计算题
1道
设置组卷 进入组卷
初中数学
同步卷 专题卷 中考卷 阶段卷 去组卷 共享课件 共享练考 共享学校
(1)
组卷设置 进入组卷

服务热线

400-816-0029

    自建题库，必找德优

德优题库QQ交流群

首页 > 试卷详情
德优网2024陕西省西安市未央区西安中学高中数学考试月考高二上

2024-2025学年陕西省西安中学高二（上）月考数学试卷（12月份）

试卷总分:88分    命题人:dygzsxyn    考试时长:120分钟

一、选择题(11小题共28分)
1. （本题2分） 椭圆x2+2y2＝1的焦点坐标为（　　）
A.（﹣1，0）和（1，0）            B.（0，﹣1）和（0，1）                                       
C.和       D.和
 
解析 纠错 收藏 下载 相似 组卷
2. （本题2分） 若方程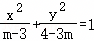表示双曲线，则实数m的取值范围为（　　）
A.        B. 
C.       D.
 
解析 纠错 收藏 下载 相似 组卷
3. （本题2分） 已知数列{an}满足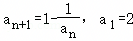，则a2024＝（　　）
A.﹣1       
B.．2        
C.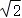       
D.．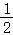
 
解析 纠错 收藏 下载 相似 组卷
4. （本题2分） P是双曲线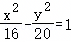上一点，F1，F2分别是双曲线左右焦点，若|PF1|＝9，则|PF2|＝（　　）
A.1                             B.17   
C.1或17                        D.以上答案均不对
 
解析 纠错 收藏 下载 相似 组卷
5. （本题2分） 已知数列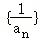是首项为5，公差为2的等差数列，则a11＝（　　）
A.       
B.        
C.       
D.
 
解析 纠错 收藏 下载 相似 组卷
6. （本题2分） 已知直线y＝kx与双曲线C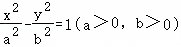：的左、右两支分别交于A、B两点，F为双曲线的右焦点，其中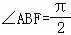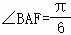，，则双曲线C的离心率e＝（　　）
A.2         
B.     
C.       
D.
 
解析 纠错 收藏 下载 相似 组卷
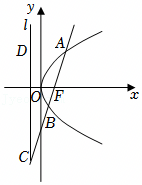
7. （本题2分） 如图，过抛物线y2＝2px（p＞0）的焦点F的直线与抛物线交于A，B两点，与其准线l交于点C（点B位于A，C之间）且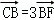，AD⊥l于点D且|AD|＝4，则|OF|等于（　　）

A.        
B.         
C.        
D.
 
解析 纠错 收藏 下载 相似 组卷
8. （本题2分） 古希腊数学家欧几里得在《几何原本》中描述了圆锥曲线的共性，并给出了圆锥曲线的统一定义，只可惜对这一定义欧几里得没有给出证明．经过了500年，到了3世纪，希腊数学家帕普斯在他的著作《数学汇篇》中，完善了欧几里得关于圆锥曲线的统一定义，并对这一定义进行了证明．他指出，到定点的距离与到定直线的距离的比是常数e的点的轨迹叫做圆锥曲线；当0＜e＜1时，轨迹为椭圆；当e＝1时，轨迹为抛物线；当e＞1时，轨迹为双曲线．现有方程m（x2+y2+2y+1）＝（x﹣2y+3）2表示的曲线是双曲线，则m的取值范围为（　　）
A.（0，1）   
B.（1，+∞）  
C.（0，5）   
D.（5，+∞）
 
解析 纠错 收藏 下载 相似 组卷
9. （本题4分） 已知数列{an}的通项公式an＝n+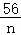，若an≥ak对n∈N*恒成立，则满足条件的正整数k可以为（　　）
A.6         
B.7         
C.．8       
D.9
 
解析 纠错 收藏 下载 相似 组卷
10. （本题4分） 已知圆C：（x+2）2+y2＝4直线l：（m+1）x+4y﹣1+m＝0（m∈R），则下列说法正确的是（　　）

A.直线l恒过定点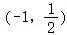 

B.直线l与圆C有两个交点  

C.当m＝1时，圆C上恰有四个点到直线l的距离等于1  

D.过直线l的平行线3x+4y﹣7m＝0上一动点P作圆C的一条切线，切点为A，则|PA|min＝4

 
解析 纠错 收藏 下载 相似 组卷
11. （本题4分） 已知椭圆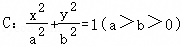的离心率为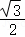，短轴长为2，P为椭圆上任意一点，F1，F2分别为椭圆的左、右焦点，则下列说法正确的是（　　）

A.过点F1的直线与椭圆交于A，B两点，则△ABF2的周长为8  

B.存在点P，使得PF1的长度为4  

C.椭圆上存在4个不同的点P，使得PF1⊥PF2   

D.．△PF1F2内切圆半径的最大值为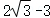

 
解析 纠错 收藏 下载 相似 组卷
二、填空题(3小题共12分)
12. （本题4分） 抛物线的焦点为 　      　．
 
解析 纠错 收藏 下载 相似 组卷
13. （本题4分） 双曲线＝1与直线l：y＝﹣x+m（m∈R）的公共点个数 　      　．
 
解析 纠错 收藏 下载 相似 组卷
14. （本题4分） 若直线y＝2x+b与曲线恰有一个公共点，则b的取值范围为 　     　．
 
解析 纠错 收藏 下载 相似 组卷
三、解答题(5小题共48分)
15. （本题8分） 已知A（0，0），B（8，﹣6），圆C是以线段AB为直径的圆，圆C2：x2+（y+2）2＝4．
（1）求圆C1的方程；
（2）判断圆C1与圆C2的位置关系并说明理由；若相交，求两圆公共弦的长．
 
解析 纠错 收藏 下载 相似 组卷
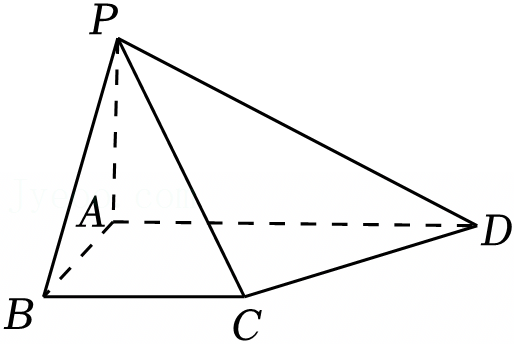
16. （本题8分） 如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，PB与底面ABCD所成角为45°，底面ABCD为直角梯形，∠ABC＝∠BAD＝90°，AD＝2，PA＝BC＝1．
（1）求PB与平面PCD所成角的正弦值；
（2）求平面PCD与平面PBA所成角的余弦值；

 
解析 纠错 收藏 下载 相似 组卷
17. （本题8分） 已知椭圆C1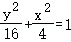：，椭圆C2以C1的短轴为长轴且与C1有相同的离心率．
（1）求椭圆C2的方程；
（2）设O为坐标原点，点A，B分别在C1，C2上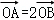，，求直线AB的方程．
 
解析 纠错 收藏 下载 相似 组卷
18. （本题12分） 已知直线l经过抛物线y2＝4x的焦点F，且与抛物线交于A，B两点．
（1）若|AF|＝4，求点A的坐标；
（2）求线段AB长的最小值．
（3）过抛物线顶点O作两条相互垂直的直线OM，ON分别交抛物线于M，N．证明：直线MN过定点．
 
解析 纠错 收藏 下载 相似 组卷
19. （本题12分） 彗星是太阳系大家庭里特殊的一族成员，它们以其明亮的尾巴和美丽的外观而闻名，它的运行轨道和行星轨道很不相同，一般为极扁的椭圆形、双曲线或抛物线．它们可以接近太阳，但在靠近太阳时，由于木星、土星等行星引力的微绕造成了轨道参数的偏差，使得它轨道的离心率由小于1变为大于或等于1，这使得少数彗星会出现“逃逸”现象，终生只能接近太阳一次，永不复返．通过演示，现有一颗彗星已经“逃逸”为以太阳为其中一个焦点，离心率为2的运行轨道，且慧星距离太阳的最近距离为1．
（1）若焦点的位置在x轴，求彗星“逃逸”轨道C的标准方程；
（2）设直线l过C的一个焦点，且与C交于A，B两点，当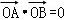时，求|AB|的值．
 
解析 纠错 收藏 下载 相似 组卷
转载声明：
本题解析属于发布者收集录入，如涉及版权请向平台申诉！ ！版权申诉

dygzsxyn

2024-12-23

高中数学 | 考试 | 难度:2.11

  • 下载量
  • 浏览量
  • 收益额
  • 0
  • 10
  • 0
同类试卷 更多>>

2023-2024学年陕西省西安市长安一中高三（上）第二次质检数学试卷（理科）

    更新:2023-12-15 12:58浏览量:7

2024-2025学年陕西省西安市铁一中学高一（上）第一次月考数学试卷

    更新:2024-10-26 12:41浏览量:123

2024-2025学年陕西师大附中高一（上）月考数学试卷（12月份）

    更新:2024-12-16 04:45浏览量:6

2024-2025学年陕西师大附中高二（上）月考数学试卷（12月份）

    更新:2024-12-29 01:34浏览量:14

2024-2025学年陕西师大附中高二（上）月考数学试卷（10月份）

    更新:2024-10-30 09:24浏览量:8

2024-2025学年陕西省西安市高新一中高二（上）第二次月考数学试卷

    更新:2024-12-27 01:45浏览量:11

2024-2025学年陕西省西安中学高三（上）第二次质检数学试卷

    更新:2024-12-28 03:32浏览量:6

2024-2025学年陕西省西安中学高二（上）月考数学试卷（12月份）

    更新:2024-12-23 07:46浏览量:10

2024-2025学年陕西省西安西北工大附中高一（上）第二次月考数学试卷（12月份）

    更新:2024-12-29 01:12浏览量:8

2024-2025学年陕西省西安市长安一中高三（上）第四次月考数学试卷

    更新:2024-02-12 04:00浏览量:8
试题下载
试题内容
调用试题名称
共享人
唐老师
试题题型
解答题
试题难度
试题题源
2020*西工大*期末
下载次数
168次
下载金币
5德优币（当前结余18德优币）
温馨提示
该试题下载至自主题库后，下载、备课永久免费！
相似题
试卷设置
试卷名称
省市校区
阶段科目
年份卷型
选择类型
已选考点
在线训练
是 否
可见权限
会员看题 会员看题和答案 无
试卷下载
试卷名称
调用试卷名称
共享人
唐老师
试卷卷型
1111
试卷难度
试卷来源
2020*西工大*期末
下载次数
168次
下载金币
5德优币（当前结余18德优币）
温馨提示
该试卷下载至自主题库后，下载、备课永久免费！
组卷付费
试卷名称
调用试卷名称
试卷来源
唐老师
试卷形式
全选 卷主 序号 卷型 难度 年份 省市区 题源 金币 操作
8 选择题 2018年 陕西 真题 2币 查看
8 选择题 2018年 陕西 真题 2币 查看
8 选择题 2018年 陕西 真题 2币 查看
8 选择题 2018年 陕西 真题 2币 查看
8 选择题 2018年 陕西 真题 2币 查看
8 选择题 2018年 陕西 真题 2币 查看
下载金币
5德优币（当前结余18德优币）
温馨提示
该试卷下载至自主题库后，下载、备课永久免费！
试题找茬
纠错类型
纠错描述
温馨提示
共享试题、试卷经平台审核通过后方可展示，并永久享用用户下载分红权！
平行组卷明细
2024-2025学年陕西省西安中学高二（上）月考数学试卷（12月份）的细目表
  • 题号
  • 考点
  • 操作
  • 1
  • 椭圆的焦点和焦距，
  • 查看
  • 2
  • 双曲线的几何特征，
  • 查看
  • 3
  • 数列递推式，
  • 查看
  • 4
  • 双曲线的焦点和焦距，
  • 查看
  • 5
  • 等差数列的通项公式，
  • 查看
  • 6
  • 双曲线的几何特征，
  • 查看
  • 7
  • 直线与椭圆的综合，
  • 查看
  • 8
  • 双曲线的几何特征，
  • 查看
  • 9
  • 数列的函数特性，数列与不等式的综合，
  • 查看
  • 10
  • 恒过定点的直线，直线与圆的位置关系，
  • 查看
  • 11
  • 直线与椭圆的综合，
  • 查看
  • 12
  • 抛物线的焦点与准线，
  • 查看
  • 13
  • 直线与双曲线的综合，
  • 查看
  • 14
  • 直线与圆的位置关系，
  • 查看
  • 15
  • 圆与圆的位置关系及其判定，
  • 查看
  • 16
  • 空间向量法求解直线与平面所成的角，空间向量法求解二面角及两平面的夹角，
  • 查看
  • 17
  • 直线与椭圆的综合，
  • 查看
  • 18
  • 直线与抛物线的综合，
  • 查看
  • 19
  • 平面向量数量积的性质及其运算，直线与双曲线的综合，轨迹方程，
  • 查看
细目重组明细
2024-2025学年陕西省西安中学高二（上）月考数学试卷（12月份）的细目表
  • 题号
  • 考点
  • 选题
  • 1
  • 椭圆的焦点和焦距，
  • 查看
  • 2
  • 双曲线的几何特征，
  • 查看
  • 3
  • 数列递推式，
  • 查看
  • 4
  • 双曲线的焦点和焦距，
  • 查看
  • 5
  • 等差数列的通项公式，
  • 查看
  • 6
  • 双曲线的几何特征，
  • 查看
  • 7
  • 直线与椭圆的综合，
  • 查看
  • 8
  • 双曲线的几何特征，
  • 查看
  • 9
  • 数列的函数特性，数列与不等式的综合，
  • 查看
  • 10
  • 恒过定点的直线，直线与圆的位置关系，
  • 查看
  • 11
  • 直线与椭圆的综合，
  • 查看
  • 12
  • 抛物线的焦点与准线，
  • 查看
  • 13
  • 直线与双曲线的综合，
  • 查看
  • 14
  • 直线与圆的位置关系，
  • 查看
  • 15
  • 圆与圆的位置关系及其判定，
  • 查看
  • 16
  • 空间向量法求解直线与平面所成的角，空间向量法求解二面角及两平面的夹角，
  • 查看
  • 17
  • 直线与椭圆的综合，
  • 查看
  • 18
  • 直线与抛物线的综合，
  • 查看
  • 19
  • 平面向量数量积的性质及其运算，直线与双曲线的综合，轨迹方程，
  • 查看
视频讲解
温馨提示
视频讲解正在加载中、请等待！
视频解析购买
支付方式
德优币数
本次消耗0德优币
温馨提示

客服电话：400-816-0029，服务邮箱：610066832@qq.com

视频资源

选择考点
存放类型
已选考点

平行组卷卷生成中,请等待

组卷异常提醒
温馨提示
试题篮存在未完成组卷，请前往组卷页面-组卷管理，点击“完成组卷”后，方可修改或添加试卷！