一、选择题(12小题共60分)
1.
(本题5分)
设全集U={﹣2,﹣1,0,1,2,3},集合A={﹣1,2},B={x|x2﹣4x+3=0},则∁U(A∪B)=( )
A.{1,3}
B.{0,3}
C..{﹣2,1}
D..{﹣2,0}
2.
(本题5分)
已知复数z满足z+z•i=2(其中i为虚数单位),则z的虚部为( )
3.
(本题5分)
已知a=e1n2,b=log34,c=21.1,则( )
A..a>b>c
B.c>a>b
C..a>c>b
D.c>b>a
4.
(本题5分)
已知向量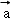 ,
,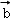 满足|
满足|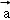 |=1,|
|=1,|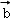 |=2,|
|=2,|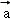 ﹣2
﹣2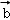 |=
|=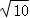 ,则
,则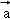 •
• =( )
=( )
5.
(本题5分)
已知双曲线E: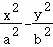 =1(a>0,b>0)以正方形ABCD的两个顶点为焦点,且经过该正方形的另两个顶点,若正方形ABCD的边长为2,则E的实轴长为( )
=1(a>0,b>0)以正方形ABCD的两个顶点为焦点,且经过该正方形的另两个顶点,若正方形ABCD的边长为2,则E的实轴长为( )
6.
(本题5分)
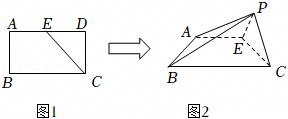
已知α,β,γ是三个不同的平面,m,n是两条不同的直线,下列命题为真命题的是( )
|
A.若m∥α,m∥β,则α∥β
|
B.若m∥α,n∥α,则m∥n
|
|
C.若m⊥α,n⊥α,则m∥n
|
D.若α⊥γ,β⊥γ,则α∥β
|
7.
(本题5分)
A..必要不充分条件
|
B.充分不必要条件
|
C..充要条件
|
D.既不充分也不必要条件
|
8.
(本题5分)
若x=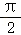 是函数f(x)=cosωx(ω≠0)图象的对称轴,则f(x)的最小正周期的最大值是( )
是函数f(x)=cosωx(ω≠0)图象的对称轴,则f(x)的最小正周期的最大值是( )
A..π
B..2π
C..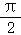
D..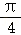
9.
(本题5分)
魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法.所谓割圆术,就是以圆内接正多边形的面积,来无限逼近圆面积.刘徽形容他的割圆术说:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.”某学生在一圆盘内画一内接正十二边形,将100粒豆子随机撒入圆盘内,发现只有4粒豆子不在正十二边形内.据此实验估计圆周率的近似值为( )
10.
(本题5分)
在公差大于0的等差数列{an}中,2a7﹣a13=1,且a1,a3﹣1,a6+5成等比数列,则数列{(﹣1)n﹣1an}的前21项和为( )
A..21
B..﹣21
C..441
D..﹣441
11.
(本题5分)
椭圆C: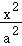 +
+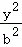 =1(a>b>0)的左顶点为A,点P,Q均在C上,且关于y轴对称.若直线AP,AQ的斜率之积为
=1(a>b>0)的左顶点为A,点P,Q均在C上,且关于y轴对称.若直线AP,AQ的斜率之积为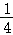 ,则C的离心率为( )
,则C的离心率为( )
12.
(本题5分)
已知实数a、b,满足a=log56+log2625,3a+4a=5b,关于a、b下列判断正确的是( )
A.a<b<2
B..b<a<2
C..2<a<b
D..2<b<a