一、选择题(12小题共60分)
1.
(本题5分)
已知集合A={x|x2<x+2},B={x|x<a},若A⊆B,则实数a的取值范围为( )
A.(﹣∞,﹣1]
B.(﹣∞,2]
C.[2,+∞)
D..[﹣1,+∞)
2.
(本题5分)
已知复数z1,z2在复平面内对应的点分别为(1,﹣1),(0,1),则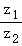 的共轭复数为( )
的共轭复数为( )
A..1+i
B..﹣1+i
C.﹣1﹣i
D..1﹣i
3.
(本题5分)
等比数列{an}的各项均为正数,且a1a5=4,则log2a1+log2a2+log2a3+log2a4+log2a5=( )
4.
(本题5分)
若干年前,某老师刚退休的月退休金为4000元,月退休金各种用途占比统计图如下面的条形图.该老师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元,则目前该老师的月退休金为( )
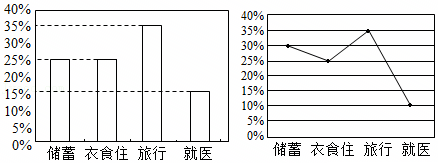
A.5000元
B..5500元
C..6000元
D..6500元
5.
(本题5分)
函数f(x)=(x3﹣3x)•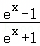 的图象大致是( )
的图象大致是( )
6.
(本题5分)
已知曲线y=ex﹣1在x=x0处的切线方程为ex﹣y+t=0,则( )
A.x0=1,t=﹣1
B..x0=1,t=﹣e
C.x0=﹣1,t=﹣1
D..x0=﹣1,t=﹣e
7.
(本题5分)
若数列{Fn}满足F1=1,F2=1,Fn=Fn﹣1+Fn﹣2(n≥3),则{Fn}称为斐波那契数列,它是由中世纪意大利数学家斐波那契最先发现.它有很多美妙的特征,如当n≥2时,前n项之和等于第n+2项减去第2项;随着n的增大,相邻两项之比越来越接近0.618.若第30项是832040,请估计这个数列的前30项之和最接近( )(备注:0.6182≈0.38,1.6182≈2.61)
A.31万
B.51万
C..217万
D..317万
8.
(本题5分)
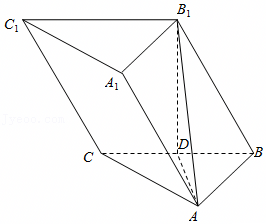
已知P,Q分别是正方体ABCD﹣A1B1C1D1的棱BB1,CC1上的动点(不与顶点重合),则下列结论错误的是( )
A.AB⊥PQ
B.AD1与PQ不会相交
C.四面体ABPQ的体积为定值
D.AP∥平面CDD1C1
9.
(本题5分)
若点P为圆x2+y2=1上的一个动点,点A(﹣1,0),B(1,0)为两个定点,则|PA|+|PB|的最大值是( )
A.2
B.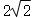
C.4
D.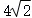
11.
(本题5分)
如图,已知直三棱柱ABC﹣A1B1C1中,底面△ABC是边长为3的正三角形,则三棱柱外接球的体积与内切球的体积比为( )

12.
(本题5分)
已知函数定义在R上的奇函数,当x<0时,f(x)=ex(x+1),给出下列命题:
①当x>0时,f(x)=ex(1﹣x)
②函数有2个零点
③f(x)>0的解集为(﹣1,0)∪(1,+∞)
④∀x1,x2∈R,都有|f(x1)﹣f(x2)|<2,
其中正确的命题是( )