德优网2023陕西省西安市碑林区西工大附中高中数学考试月考高一上
2023-2024学年陕西省西安市西工大附中高一（上）第二次月考数学试卷
试卷总分:150分
命题人:dygzsxyn
考试时长:120分钟
一、选择题(8小题共40分)
1.
（本题5分）
如图，已知矩形U表示全集，A、B是U的两个子集，则阴影部分可表示为（ ）
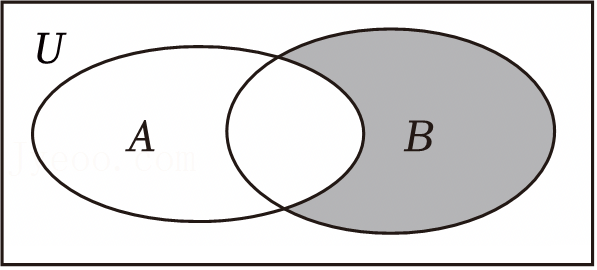
A.（∁UA）∩B
B.∁U（A∩B）
C.∁B（A∩B）
D.．∁（A∪B）A
2.
（本题5分）
函数f（x）＝log2x+2x﹣7的零点一定位于区间（ ）
A.（1，2）
B.（2，3）
C.（3，4）
D.．（5，6）
3.
（本题5分）
函数f（x）满足f（1﹣2x）＝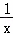
，则f（2）＝（ ）
A.2
B.﹣2
C.．
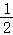
D.．﹣
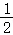
4.
（本题5分）
函数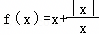
的图象是（ ）
5.
（本题5分）
已知角α是第二象限角，且|cos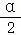
|＝﹣cos
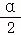，则角
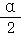是（ ）
A.第一象限角
B.第二象限角
C.．第三象限角
D.．第四象限角
6.
（本题5分）
历史上数学计算方面的三大发明是阿拉伯数、十进制和对数，其中对数的发明，大大缩短了计算时间，为人类研究科学和了解自然起了重大作用，对数运算对估算“天文数字”具有独特优势．已知lg2≈0.301，lg5≈0.699，则2.51002的估算值为（ ）
A.10199
B.10699
C.10399
D.10398
7.
（本题5分）
设a＝log32，b＝log53，c＝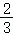
，则（ ）
A.a＜c＜b
B.a＜b＜c
C.b＜c＜a
D.．c＜a＜b
8.
（本题5分）
设函数y＝f（x）（x≠0），对于任意正数x1，x2（x1≠x2）都有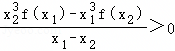
，已知函数y＝f（x﹣1）的图象关于（1，0）中心对称，若f（1）＝1，则f（x）≥x3的解集为（ ）
|
A.[﹣1，0）∪（0，1]
|
B.（﹣∞，﹣1]∪（0，1]
|
|
C.．（﹣∞，﹣1]∪[1，+∞）
|
D.[﹣1，0）∪[1，+∞）
|
二、多选题(4小题共20分)
9.
（本题5分）
下列函数值符号为正的是（ ）
A.．sin155°
B.．cos225°
C.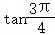
D.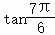
10.
（本题5分）
已知a，b∈R，且a＜b＜0，则（ ）
A.a2＜b2
B.a3＜b3
C.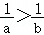
D.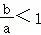
11.
（本题5分）
下列函数中，既是奇函数，又在区间（0，+∞）上单调递增的有（ ）
12.
（本题5分）
设函数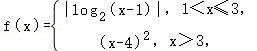
若f（x）＝a有四个实数根x1，x2，x3，x4，且x1＜x2＜x3＜x4，则
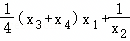的值不可以是（ ）
三、填空题(4小题共20分)
13.
（本题5分）
函数y＝ax﹣1﹣3，（a＞0且a≠1）的图象恒过定点 ．
14.
（本题5分）
已知函数f（x）为定义在R上的奇函数，且x＞0时，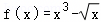
，则x＜0时，f（x）＝ ．
15.
（本题5分）
化简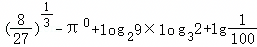
＝
16.
（本题5分）
已知函数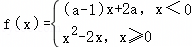
有最小值，则a的取值范围是 ．
四、解答题(6小题共70分)
17.
（本题10分）
已知角θ的终边上一点P（﹣2，a）（a≠0），且|OP|＝3（O为坐标原点），
（1）求a的值；
（2）若lg（sinθ）有意义，求tanθ的值．
18.
（本题12分）
已知一扇形的圆心角为α（0＜α＜2π），所在圆的半径R．
（1）当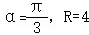
，求其弧所在弓形的面积．
（2）若该扇形的面积为S＝4，当它的圆心角和半径取何值时，该扇形的周长C最小？最小值是多少？
19.
（本题12分）
已知函数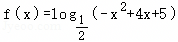
．
（1）求f（x）的定义域；
（2）若函数f（x）在（3m﹣2，m+2）上单调递增，求实数m的取值范围．
20.
（本题12分）
设命题p：幂函数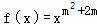
在（0，+∞）上减函数，命题q：mx2+4mx﹣4＜0对任意实数x恒成立．
（1）若命题q为真命题，求实数m的取值范围；
（2）若命题p和q中有且只有一个是真命题，求实数m的取值范围．
21.
（本题12分）
已知函数f（x）＝logax（a＞0，且a≠1）．
（1）若函数f（x）的图象与函数g（x）的图象关于直线y＝x对称，且点P（﹣3，8）在函数g（x）的图象上，求实数a的值；
（2）在（1）的条件下，不等式f（m2x）＜2f（x+2m﹣6）在x∈[4，9]上恒成立，求实数m的取值范围．
22.
（本题12分）
已知函数f（x）与g（x）具有如下性质：
①f（x）为奇函数，g（x）为偶函数；
②f（x）+g（x）＝ex（常数e是自然对数的底数，e＝2.71828…）．
利用上述性质，解决以下问题：
（1）求函数f（x）与g（x）的解析式；
（2）证明：对任意实数x，[f（x）]2﹣[g（x）]2为定值；
（3）已知m∈R，记函数y＝2m•g（2x）﹣4f（x），x∈[0，ln2]的最小值为φ（m），求φ（m）．
转载声明：
本题解析属于发布者收集录入，如涉及版权请向平台申诉！
！版权申诉
解析
纠错
收藏
下载
相似
组卷
