设命题幂函数在上减函数命题对任意实数恒成立若命题为真命题求实数的取值范围若命题和中有且只有一个是真命题求实数的取值范围

首页 > 试题列表 > 单题解析

232069. （2023•西工大附中•高一上二月）设命题p：幂函数

在（0，+∞）上减函数，命题q：mx²+4mx﹣4＜0对任意实数x恒成立．
（1）若命题q为真命题，求实数m的取值范围；
（2）若命题p和q中有且只有一个是真命题，求实数m的取值范围．

共享时间:2023-12-17 难度:3

纠错

下载

相似

组卷白板

[考点]

复合命题及其真假，一元二次不等式恒成立问题，幂函数的单调性与最值，

[答案]

（1）（﹣1，0]；

（2）（﹣2，﹣1]∪{0}．

[解析]

解：（1）命题q：mx²+4mx﹣4＜0对任意实数x恒成立，
当m＝0时，不等式为﹣4＜0恒成立，满足题意；
当m≠0时，方程mx²+4mx﹣4＝0的判别式Δ＝16m²+16m＝16m（m+1），
要使二次不等式mx²+4mx﹣4＜0恒成立，
则m＜0且Δ＜0，由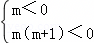

解得﹣1＜m＜0；
综上，命题q为真命题，则﹣1＜m≤0，所以实数m的取值范围为（﹣1，0]；
（2）命题p：幂函数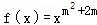

在（0，+∞）上减函数．
则m²+2m＜0，解得﹣2＜m＜0①，
命题p和q中有且只有一个是真命题，则p真q假或p假q真．
当p真q假时，由q假得m≤﹣1或m＞0②
联立①②解不等式组得，﹣2＜m≤﹣1；
当q真p假时，由q真得﹣1＜m≤0③，p假得m≤﹣2或m≥0④，
联立③④解不等式组得m＝0；
综上所述，若命题p和q中有且只有一个是真命题，则实数m的取值范围为（﹣2，﹣1]∪{0}．

[点评]

本题考查了"复合命题及其真假，一元二次不等式恒成立问题，幂函数的单调性与最值，"，属于"典型题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

166349. （2024•西工大附中•高一上二月）已知命题p：对任意x＞0，y＞0且

，不等式a²+30a≤9x+3y恒成立；命题q：∃x∈R，x²﹣2x﹣3＜a．
（1）若命题p为真命题，求实数a的取值范围；
（2）若命题p和命题q中至少有一个为真命题，求实数a的取值范围．

共享时间:2024-12-29 难度:1 相似度:1.33

解析

纠错

下载

组卷白板

235981. （2020•交大附中•高二上期末）已知命题p：∀x∈R，x²+x﹣m≥0，命题q：实数m满足：方程

表示双曲线．
（Ⅰ）若命题p为真命题，求实数m的取值范围；
（Ⅱ）若命题“p或q”为假命题，求实数m的取值范围．

共享时间:2020-02-16 难度:1 相似度:1.33

解析

纠错

下载

组卷白板

237123. （2022•西工大附中•高二下期末）已知命题p：函数y＝x²﹣2x+a在区间（1，2）上有1个零点；命题q：函数y＝x²+（2a﹣3）x+1与x轴交于不同的两点．如果p∧q是假命题，p∨q是真命题，求a的取值范围．

共享时间:2022-07-01 难度:1 相似度:1.33

解析

纠错

下载

组卷白板

236886. （2015•西安一中•高二上期末）已知p：∀x∈R，不等式x²﹣mx+

＞0恒成立，q：椭圆

＝1的焦点在x轴上，若“p或q”为真，“p且q”为假，求实数m的取值范围．

共享时间:2015-02-12 难度:1 相似度:1.33

解析

纠错

下载

组卷白板

236864. （2015•西安一中•高二上期末）已知a＞0，a≠1，设p：函数y＝log_ax在（0，+∞）上单调递减，q：曲线y＝x²+（2a﹣3）x+1与x轴交于不同的两点．若“p且q”为假，“非q”为假，求a的取值范围．

共享时间:2015-02-25 难度:1 相似度:1.33

解析

纠错

下载

组卷白板

236713. （2016•西北大附中•高二下期末）已知a＞0，设命题p：函数y＝a^x在R上调单调递增；q：不等式ax²﹣ax+1＞0对任意x∈R恒成立，若“p或q为真，p且q为假，求a的取值范围．

共享时间:2016-07-10 难度:1 相似度:1.33

解析

纠错

下载

组卷白板

170661. （2021•长安区一中•高二上期末）已知p：对任意实数x都有ax²＞﹣ax﹣1恒成立，q：关于x的方程2x²﹣3x+a＝0有实数根．若“p∨q”为真，“p∧q”为假，求实数a的取值范围．

共享时间:2021-02-18 难度:1 相似度:1.33

解析

纠错

下载

组卷白板

170791. （2020•西安中学•高二上期末）已知命题p：方程x²﹣2

x+m＝0有两个不相等的实数根；命题q：2^m⁺¹＜4．
（1）若p为真命题，求实数m的取值范围；
（2）若p∨q为真命题，p∧q为假命题，求实数m的取值范围．

共享时间:2020-02-24 难度:1 相似度:1.33

解析

纠错

下载

组卷白板

166699. （2024•高新一中•高一上一月）（1）已知a＞0，设命题p：a＞1；命题q：不等式ax²﹣ax+1＞0对∀x∈R恒成立，若“p∧q”为假，“p∨q”为真，求a的取值范围．
（2）设m∈Z，命题p：关于x的一元二次方程mx²﹣4x+4＝0的根都是整数；命题q：关于x的一元二次方程x²﹣4mx+4m²﹣4m﹣5＝0的根都是整数，试求p∧q为真命题的的充要条件．

共享时间:2024-10-24 难度:1 相似度:1.33

解析

纠错

下载

组卷白板

236691. （2016•交大附中•高二上期末）设命题p：方程

＝1表示双曲线；命题q：∃x₀∈R，x₀²+2mx₀+2﹣m＝0
（Ⅰ）若命题p为真命题，求实数m的取值范围；
（Ⅱ）若命题q为真命题，求实数m的取值范围；
（Ⅲ）求使“p∨q”为假命题的实数m的取值范围．

共享时间:2016-02-10 难度:2 相似度:0.83

解析

纠错

下载

组卷白板

236371. （2017•长安区一中•高二上期末）已知p：“直线x+y﹣m＝0与圆（x﹣1）²+y²＝1相交”；q：“方程mx²﹣x+m﹣4＝0有一正根和一负根”．若p或q为真，非p为真，求实数m的取值范围．

共享时间:2017-02-02 难度:2 相似度:0.83

解析

纠错

下载

组卷白板

236239. （2017•西安中学•高二上期末）设命题p：方程

表示中心在原点，焦点在坐标轴上的双曲线，命题q：存在x∈R，则x²﹣4x+a＜0．
（1）写出命题q的否定；
（2）若“p或非q”为真命题，求实数a的取值范围．

共享时间:2017-02-20 难度:2 相似度:0.83

解析

纠错

下载

组卷白板

236219. （2017•西安中学•高二上期末）已知m＞0，p：（x+1）（x﹣5）≤0，q：1﹣m≤x≤1+m．
（1）若p是q的充分条件，求实数m的取值范围；
（2）若m＝5，“p∨q”为真命题，“p∧q”为假命题，求实数x的取值范围．

共享时间:2017-02-08 难度:2 相似度:0.83

解析

纠错

下载

组卷白板

232487. （2023•铁路中学•高一上一月）已知命题p：∀x∈R，mx²+1＞0，命题q：∃x∈R，x²+mx+1＜0．
（1）写出命题p的否定￢p；命题q的否定￢q；
（2）若￢p和￢q至少有一个为真命题，求实数m的取值范围．

共享时间:2023-10-29 难度:2 相似度:0.83

解析

纠错

下载

组卷白板

236085. （2018•西安中学•高二上期末）已知命题p：方程x²+mx+1＝0有两个不相等的实根；q：不等式4x²+4（m﹣2）x+1＞0的解集为R；若p或q为真，p且q为假，求实数m的取值范围．

共享时间:2018-02-17 难度:2 相似度:0.83

解析

纠错

下载

组卷白板

dygzsxyn

2023-12-17

高中数学 | 高一上 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2023-2024学年陕西省西安市西工大附中高一（上）第二次月考数学试卷

更新:2023-12-17 03:45浏览量:18

微信扫码立即登录

AI助手

普通登录

手机登录

微信扫码立即登录

AI助手