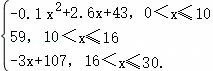首页 > 试卷详情

德优网2022陕西省西安市雁塔区师大附中高中数学考试期中高一上

2022-2023学年陕西师大附中高一（上）期中数学试卷

试卷总分:132分命题人:dygzsxyn 考试时长:120分钟

一、选择题(12小题共60分)

1. （本题5分）设全集U＝R，A＝{x∈R|﹣1＜x≤5}，B＝{x∈R|x＜2}，则A∩（∁_UB）＝（　　）

A.（﹣1，2）

B.[2，5]

C.（﹣1，2]

D.（2，5]

解析

纠错

下载

相似

组卷

2. （本题5分）命题“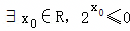

”的否定是（　　）

A.不存在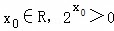	B.∀x∈R，2^x＞0
C.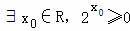．	D.∀x∈R，2^x≤0

解析

纠错

下载

相似

组卷

3. （本题5分）若“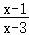

＜0”是“|x﹣a|＜2”的充分而不必要条件，则实数a的取值范围是（　　）

A.．（1，3]

B.．[1，3]

C.（﹣1，3]

D.[﹣1，3]

解析

纠错

下载

相似

组卷

4. （本题5分）若实数a，b满足0＜a＜b，且a+b＝1．则下列四个数中最大的是（　　）

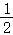
B.．a²+b²

C.2ab

D.a

解析

纠错

下载

相似

组卷

5. （本题5分）下列各组函数是同一函数的是（　　）
①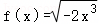

与

；
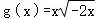②f（x）＝x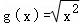与

；
③f（x）＝x⁰与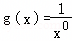

；
④f（x）＝x²﹣2x﹣1与g（t）＝t²﹣2t﹣1．

A.①②

B.．①③

C.③④

D.．①④

解析

纠错

下载

相似

组卷

6. （本题5分）设函数f（x）＝ax³+bx+1，f（1）＝1，则f（﹣1）＝（　　）

A.．﹣1

B.．0

C.．1

D.．2

解析

纠错

下载

相似

组卷

7. （本题5分）设已知函数f（x），g（x）如表所示：

x	1	2	3	4	5		x	5	4	3	2	1
f（x）	5	4	3	2	1		g（x）	4	3	2	1	5

则不等式f（g（x））＞g（f（x））的解集为（　　）

A.{1，3}	B.{5，3}
C.{2，3，4}	D.{5}

解析

纠错

下载

相似

组卷

8. （本题5分）已知函数f（x）＝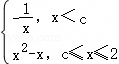

，若f（x）值域为

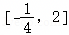，则实数c的范围是（　　）

A.	B.
C.	D.．[﹣1，+∞）

解析

纠错

下载

相似

组卷

9. （本题5分）已知非零实数a，b，c满足a＜b＜c，a+b+c＞0，则下列不等式一定成立的是（　　）

A.a+c＜2b	B.．ac＜bc
C.（c+2b）（a+2c）＞0	D.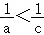

解析

纠错

下载

相似

组卷

10. （本题5分）已知函数f（x）＝x^a的图像经过点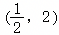

，则（　　）

A.f（x）的图像经过点（2，4）

B.f（x）的图像关于原点对称

C.．若x∈[1，2]，则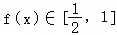

D.．当x＞0时，f（x）≥2﹣x恒成立

解析

纠错

下载

相似

组卷

11. （本题5分）以下结论正确的是（　　）

A.函数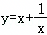的最小值是2

B.．若a，b∈R且ab＞0，则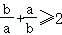

C.函数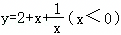的最大值为0

D.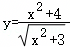．的最小值是2

解析

纠错

下载

相似

组卷

12. （本题5分）已知f（x）＝3﹣2|x|，g（x）＝x²﹣2x，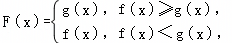

，则F（x）（　　）

A.无最小值	B.最小值﹣1
C.无最大值	D.最大值为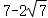

解析

纠错

下载

相似

组卷

二、填空题(4小题共16分)

13. （本题4分）函数f（x）＝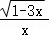

的定义域为　　．

解析

纠错

下载

相似

组卷

14. （本题4分）不等式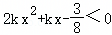

对∀x∈R都成立，那么实数k的取值范围为　　．

解析

纠错

下载

相似

组卷

15. （本题4分）为了引导居民节约用电，某城市对居民生活用电实行“阶梯电价”，按月用电量计算，将居民家庭每月用电量划分为三个阶梯，电价按阶梯递增．第一阶梯：月用电量不超过240千瓦时的部分，电价为0.5元/千瓦时；第二阶梯：月用电量超过240千瓦时但不超过400千瓦时的部分，电价为0.6元/千瓦时；第三阶梯：月用电量超过400千瓦时的部分，电价为0.8元/千瓦时．若某户居民10月份交纳的电费为360元，则此户居民10月份的用电量为　　千瓦时．

解析

纠错

下载

相似

组卷

16. （本题4分）若区间[a，b]满足：①函数f（x）在[a，b]上有定义且单调；②函数f（x）在[a，b]上的值域也为[a，b]，则称区间[a，b]为函数f（x）的共鸣区间．请写出函数f（x）＝x³的一个共鸣区间　　．

解析

纠错

下载

相似

组卷

三、解答题(5小题共56分)

17. （本题10分）设A＝{x|x²+ax﹣2＝0}，B＝{x|x²﹣3x+b＝0}，A∩B＝{1}，C＝{x|x²+2ax﹣4b＝0}．
（1）求a、b的值及A、B；
（2）求（A∪B）∩C．

解析

纠错

下载

相似

组卷

18. （本题10分）通过研究学生的学习行为，心理学家发现，学生的接受能力依赖于教师引入概念和描述问题所用的时间．讲座开始时，学生的兴趣激增；中间有一段不太长的时间，学生的兴趣保持较理想的状态，随后学生的注意力开始分散．分析结果和实验表明，用f（x）表示学生的接受能力，x表示引入概念和描述问题所用的时间（单位：分钟），可有以下的公式：
f（x）＝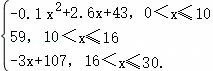

（1）开讲后多少分钟，学生的接受能力最强？能维持多长时间？
（2）一道数学难题，需要55的接受能力以及13分钟，教师能否及时在学生一直达到所需接受能力的状态下讲授完这道难题？

解析

纠错

下载

相似

组卷

19. （本题12分）已知m∈R，命题p：∀x∈R，4mx²+x+m≤0，命题q：∃x∈[1，3]，mx+1≥0．
（1）若p为假命题，求实数m的取值范围；
（2）若命题p，q有且只有一个是真命题，求实数m的取值范围．

解析

纠错

下载

相似

组卷

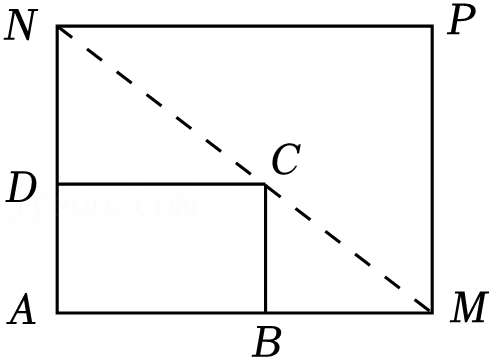
20. （本题12分）如图所示，将一个矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求M在射线AB上，N在射线AD上，且对角线MN过C点．已知AB＝6米，AD＝4米，设AN的长为x米，且要求AM的长不少于9米．
（1）设矩形花坛AMPN的面积为y，试求函数y＝f（x）的解析式及其定义域；
（2）求当AN的长度分别是多少时，矩形花坛AMPN的面积最小，并求出此最小值．

解析

纠错

下载

相似

组卷

21. （本题12分）已知f（x）是定义在[﹣1，1]上的奇函数．当a，b∈[﹣1，1]，且a+b≠0时，有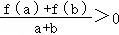

成立．
（Ⅰ）判断函数f（x）的单调性，并证明；
（Ⅱ）若f（1）＝1，且f（x）≤m²﹣2bm+1对所有x∈[﹣1，1]，b∈[﹣1，1]恒成立，求实数m的取值范围．

解析

纠错

下载

相似

组卷

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

dygzsxyn

2022-11-26

高中数学 | 考试 | 难度:1.38

下载量
浏览量
收益额

同类试卷 更多>>

2021-2022学年陕西省西安市高新三中高一（下）期中数学试卷

更新:2022-05-23 06:12浏览量:20

2024-2025学年陕西师大附中高一（下）期中数学试卷

更新:2025-05-01 03:13浏览量:55

2024-2025学年陕西师大附中高二（下）期中数学试卷

更新:2025-04-26 03:14浏览量:70

2024-2025学年陕西师大附中高二（上）期中数学试卷

更新:2024-11-18 12:41浏览量:21

2024-2025学年陕西省西安铁一中滨河高级中学高二（上）期中数学试卷

更新:2024-11-30 10:05浏览量:20

2024-2025学年陕西省西安市长安一中高一（下）期中数学试卷

更新:2025-05-02 03:14浏览量:61

2024-2025学年陕西省西安市西工大附中高二（上）期中数学试卷

更新:2024-11-30 04:49浏览量:24

2024-2025学年陕西省西安市曲江二中高一（上）期中数学试卷

更新:2024-11-24 01:26浏览量:22

2024-2025学年陕西省西安市庆安高级中学高一（上）期中数学试卷

更新:2024-11-30 01:00浏览量:19

2024-2025学年陕西省西安市临潼区华清中学高二（上）期中数学试卷

更新:2024-11-22 10:20浏览量:26

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

微信扫码立即登录

AI助手

2022-2023学年陕西师大附中高一（上）期中数学试卷

普通登录

手机登录

微信扫码立即登录

AI助手

2022-2023学年陕西师大附中高一（上）期中数学试卷