首页 | 客服 | 上传赚现
AI助手
德优题库AI助手

AI助手

搜题▪组卷

计算题
1道
设置组卷 进入组卷
初中数学
同步卷 专题卷 中考卷 阶段卷 去组卷 共享课件 共享练考 共享学校
(1)
组卷设置 进入组卷

服务热线

400-816-0029

    自建题库，必找德优

德优题库QQ交流群

首页 > 试卷详情
德优网2024陕西省西安市临潼区华清中学高中数学段考期中高二上

2024-2025学年陕西省西安市临潼区华清中学高二（上）期中数学试卷

试卷总分:150分    命题人:dygzsxyn    考试时长:120分钟

一、选择题(8小题共40分)
1. （本题5分） 直线的倾斜角为（　　）
A.30°      
B.．60°     
C.120°     
D.．150°
     
解析 纠错 收藏 下载 相似 组卷
2. （本题5分） 双曲线的焦点坐标为（　　）
A.          
B.．
C.（±3，0）
D.．（0，±3）
     
解析 纠错 收藏 下载 相似 组卷
3. （本题5分） 若两条直线l1：2x+ay﹣1＝0与l2：ax+（2a﹣1）y+3＝0相互垂直，则a＝（　　）
A.．     
B.0         
C.或0   
D.﹣2或0
     
解析 纠错 收藏 下载 相似 组卷
4. （本题5分） 已知F为双曲线C：x2﹣my2＝3m（m＞0）的一个焦点，则点F到C的一条渐近线的距离为（　　）
A.．     
B.．3        
C.．m
D.．3m
     
解析 纠错 收藏 下载 相似 组卷
5. （本题5分） 圆x2+y2﹣2x﹣8y+13＝0的圆心到直线ax+y﹣1＝0的距离为1，则a＝（　　）
A.．﹣    
B.﹣       
C.．     
D.．2
     
解析 纠错 收藏 下载 相似 组卷
6. （本题5分） 已知三棱锥O﹣ABC，点M，N分别为AB，OC的中点，且＝，＝，＝用，，表示，则等于（　　）

A.（+﹣）
B.（++）
C.．（﹣+）                    
D.．（﹣﹣）
     
解析 纠错 收藏 下载 相似 组卷
7. （本题5分） 在直三棱柱ABC﹣A1B1C1中，AC⊥BC，AC＝AA1＝4，BC＝2，则异面直线AC1与B1C所成角的余弦值为（　　）
A.      
B.．    
C.
D.
     
解析 纠错 收藏 下载 相似 组卷
8. （本题5分） 已知椭圆E：的右焦点为F（3，0），过点F的直线交椭圆于A，B两点，若AB的中点坐标为（1，﹣1），则E的方程为（　　）
A.                    B.   
C.                    D.
     
解析 纠错 收藏 下载 相似 组卷
二、多选题(3小题共18分)
9. （本题6分） 已知曲线C：mx2+ny2＝1，则（　　）

A.若m＞n＞0，则C是椭圆，其焦点在y轴上   

B.若m＝n＞0，则C是圆，其半径为

C.．若mn＜0，则C是双曲线，其渐近线方程为 

D.．若m＝0，n＞0，则C是两条直线

     
解析 纠错 收藏 下载 相似 组卷
10. （本题6分） 已知点P在圆（x﹣5）2+（y﹣5）2＝16上，点A（4，0），B（0，2），则（　　）

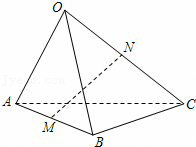
A.．点P到直线AB的距离小于10 

B.．点P到直线AB的距离大于2  

C.．当∠PBA最小时，|PB|＝3

D.．当∠PBA最大时，|PB|＝3

     
解析 纠错 收藏 下载 相似 组卷
11. （本题6分） 设点F1，F2分别为椭圆C：+＝1的左、右焦点，点P是椭圆C上任意一点，若使得•＝m成立的点恰好是4个，则实数m的取值可以是（　　）
A.1         
B.．3        
C.．5       
D.4
     
解析 纠错 收藏 下载 相似 组卷
三、填空题(3小题共15分)
12. （本题5分） 过点P（2，3）且在两坐标轴上的截距相等的直线方程为 　                  　 ．
     
解析 纠错 收藏 下载 相似 组卷
13. （本题5分） 设F1，F2为双曲线的两个焦点，点P是双曲线上的一点，且∠F1PF2＝90°，则△F1PF2的面积为 　        ．
     
解析 纠错 收藏 下载 相似 组卷
14. （本题5分） 设F1，F2为椭圆C：+＝1的两个焦点，M为C上一点且在第一象限．若△MF1F2为等腰三角形，则M的坐标为　             　 ．
     
解析 纠错 收藏 下载 相似 组卷
四、解答题(5小题共77分)
15. （本题13分） 已知点M（1，1），圆C：x2+y2＝2．
（1）若过点M的直线l与圆C相切，求直线l的方程；
（2）若直线ax﹣y+4＝0与圆C相交于A，B两点，弦AB的长为2，求a的值．
     
解析 纠错 收藏 下载 相似 组卷
16. （本题15分） 如图，在三棱柱ABC﹣A1B1C1，AC＝CB＝2，AA1＝2，且AC⊥CB，AA1⊥底面ABC，E为AB中点．
（1）求证：BC1∥平面A1CE；
（2）求二面角A1﹣CE﹣A的余弦值．

     
解析 纠错 收藏 下载 相似 组卷
17. （本题15分） 已知椭圆的离心率为，左焦点．
（1）求椭圆C的标准方程；
（2）若直线y＝x+m与椭圆C交于不同的两点A、B，且线段AB的中点M在圆x2+y2＝1上，求m的值．
     
解析 纠错 收藏 下载 相似 组卷
18. （本题17分） 已知曲线C：x2﹣y2＝1及直线l：y＝kx﹣1．且直线l与双曲线C有两个不同的交点A，B．
（1）求实数k的取值范围；
（2）O是坐标原点，且△AOB的面积为，求实数k的值．
     
解析 纠错 收藏 下载 相似 组卷
19. （本题17分） 椭圆+＝1（a＞b＞0）的右焦点F、右顶点A和上顶点B满足＝．
（1）求椭圆的离心率e；
（2）直线l与椭圆有唯一公共点M，与y轴相交于N（N异于M）．记O为坐标原点，若|OM|＝|ON|，且△MON的面积为，求椭圆的方程．
     
解析 纠错 收藏 下载 相似 组卷
转载声明：
本题解析属于发布者收集录入，如涉及版权请向平台申诉！ ！版权申诉

ds@dyw.com

2024-11-22

高中数学 | 段考 | 难度:1.79

  • 下载量
  • 浏览量
  • 收益额
  • 73
  • 47
  • 0
下载试卷 收藏
平行组卷 细目重组
试卷分析 加入白板
加卷篮 更多功能
同类试卷 更多>>

2021-2022学年陕西省西安市高新三中高一（下）期中数学试卷

    更新:2022-05-23 06:12浏览量:39

2024-2025学年陕西师大附中高一（下）期中数学试卷

    更新:2025-05-01 03:13浏览量:119

2024-2025学年陕西师大附中高二（下）期中数学试卷

    更新:2025-04-26 03:14浏览量:152

2024-2025学年陕西师大附中高二（上）期中数学试卷

    更新:2024-11-18 12:41浏览量:47

2024-2025学年陕西省西安铁一中滨河高级中学高二（上）期中数学试卷

    更新:2024-11-30 10:05浏览量:62

2024-2025学年陕西省西安市长安一中高一（下）期中数学试卷

    更新:2025-05-02 03:14浏览量:172

2024-2025学年陕西省西安市西工大附中高二（上）期中数学试卷

    更新:2024-11-30 04:49浏览量:50

2024-2025学年陕西省西安市曲江二中高一（上）期中数学试卷

    更新:2024-11-24 01:26浏览量:49

2024-2025学年陕西省西安市庆安高级中学高一（上）期中数学试卷

    更新:2024-11-30 01:00浏览量:46

2024-2025学年陕西省西安市临潼区华清中学高二（上）期中数学试卷

    更新:2024-11-22 10:20浏览量:47
温馨提示
对不起！这是别人共享的试卷，需要下载到自主题库后，可将该试卷添加到白板
试题下载
试题内容
调用试题名称
共享人
唐老师
试题题型
解答题
试题难度
试题题源
2020*西工大*期末
下载次数
168次
下载金币
5德优币（当前结余18德优币）
温馨提示
该试题下载至自主题库后，下载、备课永久免费！
相似题
德优题库校正考点说明
任务说明： 看答案选考点，根据平台试卷上的试题答案，完善每个试题的考点
单价设置： 0.05元/每题，兑换德优币0.25个/每题
结算方式： 由平台德优币兑换现金，支持银行卡、支付宝账号、微信收款码体现
温馨提示：
  • 1、自主创建平台账号，免费领取一个科目的自主题库；
  • 2、在试卷列表自主领取试卷，一次性不得超过50套；
  • 3、领取的任务超过一周未完成的，平台自动取消将资源释放给他人；
  • 4、胡乱修改考点的违规操作，平台将永久封禁该账号。
步骤1
步骤 1：打开试卷
点击“校正考点”，确认领取
步骤2
步骤 2：改考点
点击试题旁边 “改考点” 按钮
步骤3
步骤 3：重新给试题定义考点
确认考点无误后，点击“提交”按钮
步骤4
方案二：试卷“解析” 按钮 ，打开试题详情，点击改考点
可以在试卷详情，或者试题详情进行改考点
步骤4
方案二：试题详情 点击“改考点”按钮
重新给试题定义考点，点击“确认”按钮
步骤4
步骤 4：试卷详情 “提交任务”
校正完所有试题考点，提交任务 开始一套试卷
操作步骤
领取试卷→修改考点→完成任务→领取赚现
试卷设置
试卷名称
省市校区
阶段科目
年份卷型
选择类型
已选考点
在线训练
是 否
可见权限
会员看题 会员看题和答案 无
试卷下载
试卷名称
调用试卷名称
共享人
唐老师
试卷卷型
1111
试卷难度
试卷来源
2020*西工大*期末
下载次数
168次
下载金币
5德优币（当前结余18德优币）
温馨提示
该试卷下载至自主题库后，下载、备课永久免费！
组卷付费
试卷名称
调用试卷名称
试卷来源
唐老师
试卷形式
全选 卷主 序号 卷型 难度 年份 省市区 题源 金币 操作
8 选择题 2018年 陕西 真题 2币 查看
8 选择题 2018年 陕西 真题 2币 查看
8 选择题 2018年 陕西 真题 2币 查看
8 选择题 2018年 陕西 真题 2币 查看
8 选择题 2018年 陕西 真题 2币 查看
8 选择题 2018年 陕西 真题 2币 查看
下载金币
5德优币（当前结余18德优币）
温馨提示
该试卷下载至自主题库后，下载、备课永久免费！
试题找茬
纠错类型
纠错描述
温馨提示
共享试题、试卷经平台审核通过后方可展示，并永久享用用户下载分红权！
平行组卷明细
2024-2025学年陕西省西安市临潼区华清中学高二（上）期中数学试卷的细目表
  • 题号
  • 考点
  • 操作
  • 1
  • 直线的倾斜角，
  • 查看
  • 2
  • 双曲线的焦点和焦距，
  • 查看
  • 3
  • 直线的一般式方程与直线的垂直关系，
  • 查看
  • 4
  • 双曲线的几何特征，
  • 查看
  • 5
  • 点到直线的距离公式，直线与圆的位置关系，
  • 查看
  • 6
  • 空间向量的数乘及线性运算，
  • 查看
  • 7
  • 异面直线及其所成的角，
  • 查看
  • 8
  • 直线与椭圆的综合，
  • 查看
  • 9
  • 双曲线的标准方程，
  • 查看
  • 10
  • 直线与圆的位置关系，
  • 查看
  • 11
  • 椭圆的几何特征，
  • 查看
  • 12
  • 直线的截距式方程，
  • 查看
  • 13
  • 双曲线的焦点和焦距，
  • 查看
  • 14
  • 椭圆的几何特征，
  • 查看
  • 15
  • 圆的切线方程，直线与圆的位置关系，
  • 查看
  • 16
  • 直线与平面平行，二面角的平面角及求法，
  • 查看
  • 17
  • 直线与椭圆的综合，
  • 查看
  • 18
  • 双曲线的几何特征，
  • 查看
  • 19
  • 直线与椭圆的综合，
  • 查看
细目重组明细
2024-2025学年陕西省西安市临潼区华清中学高二（上）期中数学试卷的细目表
  • 题号
  • 考点
  • 选题
  • 1
  • 直线的倾斜角，
  • 查看
  • 2
  • 双曲线的焦点和焦距，
  • 查看
  • 3
  • 直线的一般式方程与直线的垂直关系，
  • 查看
  • 4
  • 双曲线的几何特征，
  • 查看
  • 5
  • 点到直线的距离公式，直线与圆的位置关系，
  • 查看
  • 6
  • 空间向量的数乘及线性运算，
  • 查看
  • 7
  • 异面直线及其所成的角，
  • 查看
  • 8
  • 直线与椭圆的综合，
  • 查看
  • 9
  • 双曲线的标准方程，
  • 查看
  • 10
  • 直线与圆的位置关系，
  • 查看
  • 11
  • 椭圆的几何特征，
  • 查看
  • 12
  • 直线的截距式方程，
  • 查看
  • 13
  • 双曲线的焦点和焦距，
  • 查看
  • 14
  • 椭圆的几何特征，
  • 查看
  • 15
  • 圆的切线方程，直线与圆的位置关系，
  • 查看
  • 16
  • 直线与平面平行，二面角的平面角及求法，
  • 查看
  • 17
  • 直线与椭圆的综合，
  • 查看
  • 18
  • 双曲线的几何特征，
  • 查看
  • 19
  • 直线与椭圆的综合，
  • 查看
视频讲解
温馨提示
视频讲解正在加载中、请等待！
视频解析购买
支付方式
德优币数
本次消耗0德优币
温馨提示

客服电话：400-816-0029，服务邮箱：610066832@qq.com

视频资源

选择考点
存放类型
已选考点

平行组卷卷生成中,请等待

组卷异常提醒
温馨提示
试题篮存在未完成组卷，请前往组卷页面-组卷管理，点击“完成组卷”后，方可修改或添加试卷！
试题改考点
原考点
选择新考点
试题