服务热线
搜题▪组卷
试卷总分:150分 命题人:dygzsxyn 考试时长:120分钟
| A..{0,1,2,3,4,5,6} |
B.{1,2,3,4,5,6} |
| C.{2,4} |
D.{x|﹣2≤x≤6} |

|
A. |
B. |
|
C.. |
D. |

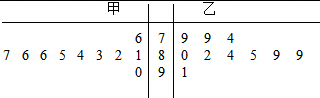
| 年度 | 2016﹣2017 | 2017﹣2018 | 2018﹣2019 | 2019﹣2020 | 2020﹣2021 | 2021﹣2022 |
| 年度代号t | 1 | 2 | 3 | 4 | 5 | 6 |
| 旅游人次y | 1.7 | 1.97 | 2.24 | 0.94 | 2.54 | 3.15 |
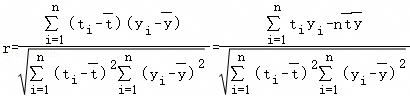 ,回归直线的斜率和截距的最小二乘估计公式分别为:
,回归直线的斜率和截距的最小二乘估计公式分别为: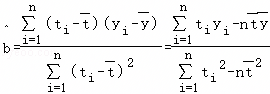 ,
,
bqf@dyw.com
2023-04-08
高中数学 | 模考 | 难度:1.39
| 下载试卷 | 收藏 |
| 平行组卷 | 细目重组 |
| 试卷分析 | 加入白板 |
| 加卷篮 | 更多功能 |
平行组卷卷生成中,请等待