首页 > 试卷详情

德优网2022陕西省西安市长安区长安区一中高中数学考试期末高二上

2021-2022学年陕西省西安市长安一中高二（上）期末数学试卷（文科）

试卷总分:150分命题人:dygzsxyn 考试时长:120分钟

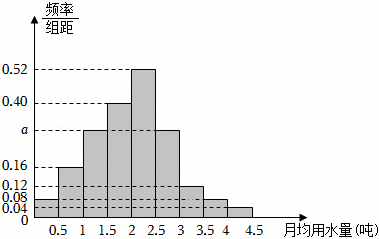
一、选择题(14小题共70分)

1. （本题5分）已知z＝2﹣i，则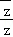

＝（　　）

C.．﹣1

D.．

解析

纠错

下载

相似

组卷

2. （本题5分）已知命题p：cos2α＝﹣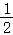

，命题q：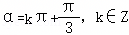

．则p是q的（　　）条件．

A.充分不必要	B.．必要不充分
C.充分必要	D.．既不充分也不必要

解析

纠错

下载

相似

组卷

3. （本题5分）设抛物线C：y²＝2px的焦点为F，准线为l．P是抛物线C上异于O的一点，过P作PQ⊥l于Q，则线段FQ的垂直平分线（　　）

A.经过点P	B.．经过点O
C.平行于直线OP	D.垂直于直线OP

解析

纠错

下载

相似

组卷

4. （本题5分）若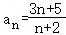

，则a_n与a_n₊₁的大小关系是（　　）

A.．a_n＞a_n₊₁

B.．a_n＜a_n₊₁

C.．a_n＝a_n₊₁

D.不能确定

解析

纠错

下载

相似

组卷

5. （本题5分）有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（　　）

A.．

B.．

解析

纠错

下载

相似

组卷

6. （本题5分）设函数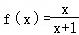

，则下列函数中为奇函数的是（　　）

A.．f（x+1）+1

B.f（x﹣1）+1

C.f（x+1）﹣1

D.．f（x﹣1）﹣1

解析

纠错

下载

相似

组卷

7. （本题5分）观察（x²）'＝2x，（x⁴）'＝4x³，y＝f（x），由归纳推理可得：若定义在R上的函数f（x）满足f（﹣x）＝f（x），记g（x）为f（x）的导函数，则g（﹣x）＝（　　）

A.．f（x）

B.．﹣f（x）

C.．g（x）

D.﹣g（x）

解析

纠错

下载

相似

组卷

8. （本题5分）若关于x的方程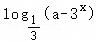

＝x﹣2有解，则实数a的取值范围为（　　）

A.[2，+∞）

B.[4，+∞）

C.[6，+∞）

D.[8，+∞）

解析

纠错

下载

相似

组卷

9. （本题5分）某路口人行横道的信号灯为红灯和绿灯交替出现，红灯持续时间为40秒．若一名行人来到该路口遇到红灯，则至少需要等待18秒才出现绿灯的概率为（　　）

C.．

解析

纠错

下载

相似

组卷

10. （本题5分）等差数列{a_n}的通项公式a_n＝2n﹣1，数列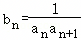

，其前n项和为S_n，则S_3n等于（　　）

A.．

C.．

D.．

解析

纠错

下载

相似

组卷

11. （本题5分）圆x²+y²﹣4x+2y+1＝0与直线y﹣2tx+2t﹣1＝0（t∈R）的位置关系为（　　）

A.．相切

B.．相离

C.相交

D.无法确定

解析

纠错

下载

相似

组卷

12. （本题5分）若a＞0，b＞0，且函数f（x）＝4x³﹣ax²﹣2bx+2在x＝1处有极值，则ab的最大值等于（　　）

A.．2

B.．3

C.．6

D.9

解析

纠错

下载

相似

组卷

13. （本题5分）已知f（x）是定义在R上的奇函数，对任意两个不相等的正数x₁，x₂，都有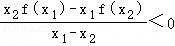

，记

，

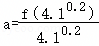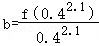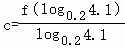，则（　　）

A.．a＜c＜b

B.a＜b＜c

C.c＜b＜a

D.．b＜c＜a

解析

纠错

下载

相似

组卷

14. （本题5分）已知双曲线C：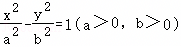

的左、右焦点分别为F₁，F₂，过点F₁且斜率为

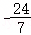的直线与双曲线在第二象限的交点为A，若（

）•

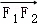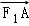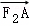＝0，则双曲线C的离心率是（　　）

A.．

C.．

D.．2

解析

纠错

下载

相似

组卷

二、填空题(6小题共30分)

15. （本题5分）我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案．通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），⋯，[4，4.5）分成9组，制成了如图所示的频率分布直方图，则a＝　．

解析

纠错

下载

相似

组卷

16. （本题5分）设2^a＝3^b＝m，且

＝2，则m＝　

解析

纠错

下载

相似

组卷

17. （本题5分）如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据（单位：件），若这两组数据的中位数相等，且平均值也相等，则x＝　　，y＝　　．

解析

纠错

下载

相似

组卷

18. （本题5分）一个六棱锥的体积为2

，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为　　．

解析

纠错

下载

相似

组卷

19. （本题5分）数学中有许多形状优美、寓意美好的曲线，曲线C：x²+y²＝1+|x|y就是其中之一（如图），给出下列三个结论：
①曲线C恰好经过6个整点（即横、纵坐标均为整数的点）；
②曲线C上任意一点到原点的距离都不超过

；
③曲线C所围成的“心形”区域的面积小于3．
其中，所有正确结论的序号是　　．

解析

纠错

下载

相似

组卷

20. （本题5分）已知函数f（x）＝2x³﹣3x，若过点M（1，m﹣1）存在三条直线与曲线y＝f（x）相切，测m的取值范围为　　．

解析

纠错

下载

相似

组卷

三、解答题(4小题共50分)

21. （本题12分）已知函数

（Ⅰ）求函数g（x）的单调递减区间；
（Ⅱ）在△ABC中，角A，B，C所对的边分别为a，b，c，且满足

，

，求△ABC面积的最大值．

解析

纠错

下载

相似

组卷

22. （本题12分）如图所示，四棱锥P﹣ABCD的底面为直角梯形，∠ADC＝∠DCB＝90°，AD＝1，BC＝3，PC＝CD＝2AD，PC⊥底面ABCD，E为AB的中点．
（Ⅰ）求证：平面PDE⊥平面PAC；
（Ⅱ）求点B到平面PDE的距离．

解析

纠错

下载

相似

组卷

23. （本题13分）已知椭圆

（a＞b＞0）的左、右焦点为F₁，F₂，|F₁F₂|＝2，离心率e为

．
（1）求椭圆C的标准方程．
（2）C的左顶点为A，过右焦点F₂的直线l交椭圆C于D，E两点，记直线l，AD，AE的斜率分别为k，k₁，k₂，求证：

．

解析

纠错

下载

相似

组卷

24. （本题13分）已知函数

在x＝0处的切线与x轴平行．
（Ⅰ）求a的值；
（Ⅱ）判断在（0，π）上零点的个数，并说明理由．

解析

纠错

下载

相似

组卷

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

dygzsxyn

2022-02-04

高中数学 | 考试 | 难度:1.46

下载量
浏览量
收益额

同类试卷 更多>>

2024-2025学年陕西师大附中高二（上）期末数学试卷

更新:2025-02-11 01:57浏览量:8

2024-2025学年陕西省西安市西工大附中高一（上）期末数学试卷

更新:2025-02-26 02:23浏览量:11

2024-2025学年陕西省西安市西工大附中高二（上）期末数学试卷

更新:2025-02-18 01:01浏览量:6

2024-2025学年陕西省西安市铁一中学高一（上）期末数学试卷

更新:2025-02-09 03:44浏览量:7

2024-2025学年陕西省西安市铁一中学高二（上）期末数学试卷

更新:2025-02-12 04:00浏览量:10

2024-2025学年陕西省西安八十五中高二（上）期末数学试卷

更新:2025-02-15 01:49浏览量:8

2023-2024学年陕西师大附中高一（下）期末数学试卷

更新:2024-07-09 03:25浏览量:6

2023-2024学年陕西师大附中高二（上）期末数学试卷

更新:2024-02-14 08:16浏览量:6

2023-2024学年陕西省西安中学高三（上）期末数学试卷（文科）

更新:2024-02-08 04:23浏览量:6

2023-2024学年陕西省西安中学高三（上）期末数学试卷（理科）

更新:2024-02-27 11:58浏览量:6

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

普通登录

手机登录

微信扫码立即登录

2021-2022学年陕西省西安市长安一中高二（上）期末数学试卷（文科）