服务热线
搜题▪组卷
试卷总分:150分 命题人:dygzsxyn 考试时长:120分钟
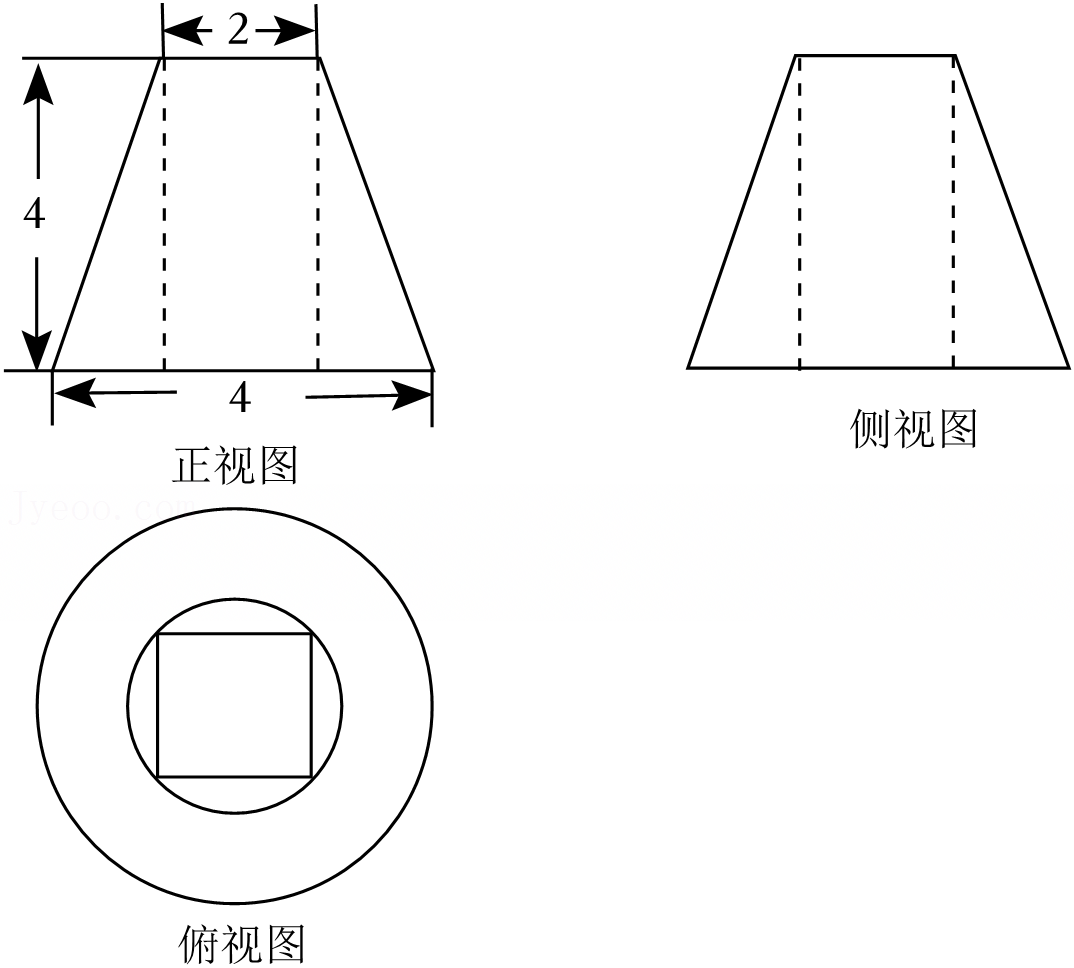
|
A.充分条件 |
B.充分不必要条件 |
|
C..必要不充分条件 |
D..既不充分也不必要条件 |
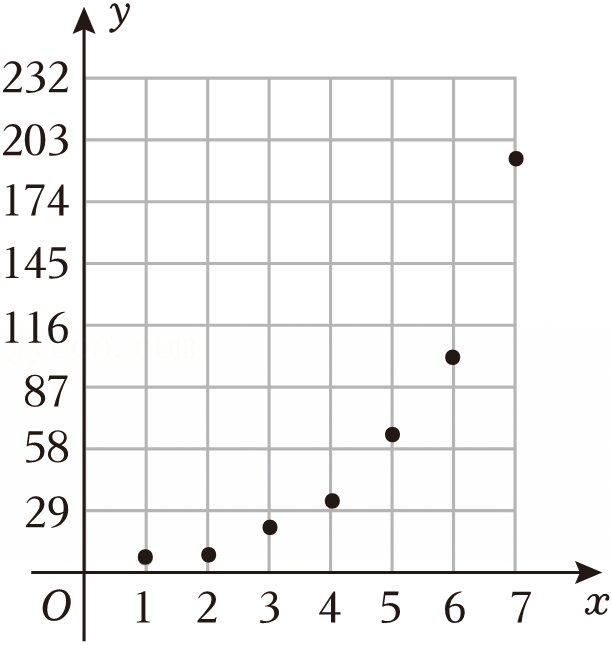
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 6 | 11 | 21 | 34 | 66 | 101 | 196 |
| 支付方式 | 现金 | 乘车卡 | 扫码 |
| 比例 | 10% | 60% | 30% |
| 100.54 | ||||
| 62.14 | 1.54 | 2535 | 50.12 | 3.47 |
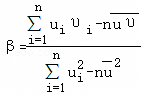 ,
,
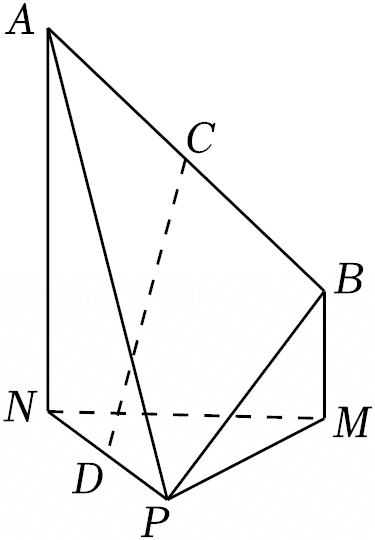

mnf@dyw.com
2023-02-15
高中数学 | 考试 | 难度:1.48
| 下载试卷 | 收藏 |
| 平行组卷 | 细目重组 |
| 试卷分析 | 加入白板 |
| 加卷篮 | 更多功能 |
平行组卷卷生成中,请等待