首页 > 试卷详情

德优网2021陕西省西安市未央区西安中学高中数学模考模拟

2021年陕西省西安中学高考数学九模试卷（文科）

试卷总分:100分命题人:dygzsxyn 考试时长:120分钟

一、选择题(12小题共36分)

1. （本题3分）已知集合A＝{y|y＝e^x}，集合B＝{﹣2，﹣1，1，2}，则A∩B＝（　　）

A.{x|1＜x＜2}

B.{1，2}

C.．{﹣1，﹣2}

D.．{x|x＞0}

解析

纠错

下载

相似

组卷

2. （本题3分）复数

的虚部为（　　）

A.．1

B.．﹣1

C.i

D.．﹣i

解析

纠错

下载

相似

组卷

3. （本题3分）某高二年级有文科学生500人，理科学生1500人，为了解学生对数学的喜欢程度，现用分层抽样的方法从该年级抽取一个容量为60的样本，则样本中文科生有（　　）人．

A.10

B.．15

C.20

D.．25

解析

纠错

下载

相似

组卷

4. （本题3分）已知直线l⊥平面α，直线m⊂平面β，则下列四个命题正确的是（　　）
①α∥β⇒l⊥m；②α⊥β⇒l∥m；③l∥m⇒α⊥β；④l⊥m⇒α∥β．

A.．②④

B.①②

C.．③④

D.．①③

解析

纠错

下载

相似

组卷

5. （本题3分）已知p：x≥k，q：

＜1，如果p是q的充分不必要条件，则实数k的取值范围是（　　）

A.．[2，+∞）

B.．（2，+∞）

C.．[1，+∞）

D.（﹣∞，﹣1]

解析

纠错

下载

相似

组卷

6. （本题3分）已知角α满足

，则tanα＝（　　）

A.．1或﹣3

B.1

C.．﹣1或3

D.．3

解析

纠错

下载

相似

组卷

7. （本题3分）如图代表未折叠正方体的展开图，将其折叠起来，变成正方体后的图形是（　　）

A.．

B.．

D.．

解析

纠错

下载

相似

组卷

8. （本题3分）等比数列{a_n}中，a₇²＝a₉且a₈＞a₉，则使得a_n﹣

＞0的自然数n的最大值为（　　）

A.．10

B.．9

C.．8

D.．7

解析

纠错

下载

相似

组卷

9. （本题3分）已知某8个数的平均数为5，方差为s²，现又加入一个新数据5，此时这9个数的平均数为

，方差为

，则（　　）

A.s²＜2，

＝5

B.s²＝2，

＝5

C.s²＞2，

＜5

D.s²＜2，

＜5

解析

纠错

下载

相似

组卷

10. （本题3分）记不等式组

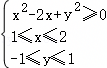表示的平面区域为Ω，P（x₁，y₁）、Q（x₂，y₂）是Ω内的任意点，则z＝（x₁﹣1）（x₂﹣1）+y₁y₂的最大值是（　　）

A.2

C.．1

D.．

解析

纠错

下载

相似

组卷

11. （本题3分）已知曲线f（x）＝sin（ωx）+

cos（ωx）（ω＞0）的两条相邻的对称轴之间的距离为

，且曲线关于点（x₀，0）成中心对称，若x₀∈[0，

]，则x₀＝（　　）

A.．

B.．

解析

纠错

下载

相似

组卷

12. （本题3分）过双曲线M：x²

＝1的左顶点A作斜率为1的直线l，若l与双曲线M的两条渐近线分别相交于B、C，且|AB|＝|BC|，则双曲线M的离心率是（　　）

B.．

C.．

D.．

解析

纠错

下载

相似

组卷

二、填空题(4小题共12分)

13. （本题3分）观察以下式子：

按此规律归纳猜想第5个的等式为　．（不需要证明）

解析

纠错

下载

相似

组卷

14. （本题3分）执行下面的程序框图，如果输入x、y∈R，那么输出z的最小值为　　

解析

纠错

下载

相似

组卷

15. （本题3分）直四棱柱ABCD﹣A₁B₁C₁D₁，高AA₁为3，底面ABCD为长方形且面积为

，则该直四棱柱外接球表面积的最小值为　．

解析

纠错

下载

相似

组卷

16. （本题3分）设圆锥曲线r的两个焦点分别为F₁，F₂，若曲线r上存在点P满足|PF₁|：|F₁F₂|：|PF₂|＝4：3：2，则曲线r的离心率等于　

解析

纠错

下载

相似

组卷

三、解答题(7小题共52分)

17. （本题7分）在△ABC中，已知A＝

，cosB＝

．
（Ⅰ）求cosC的值；
（Ⅱ）若BC＝2

，D为AB的中点，求CD的长．

解析

纠错

下载

相似

组卷

18. （本题7分）某大学生在开学季准备销售一种文具套盒进行试创业，在一个开学季内，每售出1盒该产品获利润50元，未售出的产品，每盒亏损30元．根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示．该同学为这个开学季购进了200盒该产品，以x（单位：盒）表示这个开学季内的市场需求量，y（单位：元）表示这个开学季内经销该产品的利润．
（1）根据直方图估计这个开学季内市场需求量的平均数和众数；
（2）将y表示为x的函数；
（3）根据直方图估计利润不少于3600元的概率．

解析

纠错

下载

相似

组卷

19. （本题7分）．如图，在三棱柱ABC﹣A₁B₁C₁中，点C在平面A₁B₁C₁内的射影点为A₁B₁的中点O，且AC：BC：AB：AA₁＝1：1：

：2．
（1）求证：AB⊥平面OCC₁；
（2）若CO＝

，求点C到平面ABO的距离．

解析

纠错

下载

相似

组卷

20. （本题7分）已知抛物线y²＝4x，焦点为F．
（1）若圆心在抛物线y²＝4x上的动圆，大小随位置而变化，但总是与直线x+1＝0相切，求所有的圆都经过的定点坐标；
（2）若过F点的直线与抛物线相交于M，N两点，若

，求直线MN的斜率．

解析

纠错

下载

相似

组卷

21. （本题7分）设函数

．
（1）当a＝1时，求曲线y＝f（x）在点（1，f（1））处的切线方程；
（2）若函数y＝f（x）在其定义域内为增函数，求实数a的取值范围．

解析

纠错

下载

相似

组卷

22. （本题10分）已知极坐标的极点与直角坐标系原点重合，极轴与x轴正半轴重合，曲线C的参数方程

（α为参数），曲线E的方程为

（t为参数）．
（1）求曲线C与曲线E的普通方程；
（2）曲线C上的点到曲线E的最大距离．

解析

纠错

下载

相似

组卷

23. （本题7分）已知函数f（x）＝|x+1|+|x+a|．
（1）若a＝﹣4，求函数f（x）的最小值；
（2）若存在x₀∈R，使得f（x）≤|2a+3|成立，求实数a的取值范围．

解析

纠错

下载

相似

组卷

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

dygzsxyn

2021-06-30

高中数学 | 模考 | 难度:1.7

下载量
浏览量
收益额

同类试卷 更多>>

2021年陕西省西安市西安中学高考数学二模试卷（理科）

更新:2021-03-18 12:07浏览量:488

2024-2025学年陕西省西安市高新一中高三（上）月考数学试卷（二模）

更新:2024-03-18 04:53浏览量:21

2024-2025学年陕西省西安市高新一中高三（上）第三次模拟数学试卷

更新:2024-04-04 06:23浏览量:13

2024-2025学年陕西省西安建筑科技大学附属中学高三（上）月考数学试卷（一模）

更新:2024-03-13 08:20浏览量:18

2024-2025学年陕西省西安八十五中高三（上）第一次模拟数学试卷

更新:2024-03-12 06:30浏览量:12

2024-2025年陕西省西安市高新一中高三（上）第五次模拟数学试卷

更新:2024-05-13 09:53浏览量:17

2023-2024学年陕西省西安市周至四中高三（上）月考数学试卷（理科）（一模）

更新:2023-03-04 02:06浏览量:13

2024年陕西师大附中高考数学十模试卷（理科）

更新:2024-07-09 05:34浏览量:20

2024年陕西省西安中学高考数学模拟试卷（文科）（一）

更新:2024-03-07 08:48浏览量:13

2024年陕西省西安中学高考数学模拟试卷（理科）（一）

更新:2024-03-11 01:46浏览量:14

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

微信扫码立即登录

AI助手

2021年陕西省西安中学高考数学九模试卷（文科）

普通登录

手机登录

微信扫码立即登录

AI助手

2021年陕西省西安中学高考数学九模试卷（文科）