首页 > 试卷详情

德优网2022陕西省西安市长安区长安区一中高中数学模考模拟

2022年陕西省西安市长安一中高考数学三模试卷（理科）

试卷总分:150分命题人:dygzsxyn 考试时长:120分钟

一、选择题(12小题共60分)

1. （本题5分）已知集合A＝{x|x²﹣2x＞0}，B＝{y|y＝sinx}，则（∁_RA）∩B＝（　　）

A.[0，1）

B.[﹣1，1]

C.[0，2]

D.[0，1]

解析

纠错

下载

相似

组卷

2. （本题5分）已知i为虚数单位，复数z满足z（1+2i）＝|4+3i|，则z的共轭复数

＝（　　）

A.．1﹣2i

B.1+2i

C.2﹣i

D.．2+i

解析

纠错

下载

相似

组卷

3. （本题5分）某商场2020年部分月份销售金额如表：

月份x	2	4	6	8	10
销售金额y（单位：万元）	64	132	a	286	368

若用最小二乘法求得回归直线方程为

＝38.1x﹣17.6，则a＝（　　）

A.198.2	B.．205
C.211	D.．213.5

解析

纠错

下载

相似

组卷

4. （本题5分）函数y＝

在[﹣π，π]的图象大致为（　　）

A.	B.
C.	D.

解析

纠错

下载

相似

组卷

5. （本题5分） “干支纪年法”是中国历法上使用的纪年方法．甲，乙，丙，丁，戊，己，庚，辛，壬，癸被称为“十天干”，子，丑，寅，卯，辰，巳，午，未，申，酉，戌，亥被称为“十二地支”，“天干”以“甲”字开始，“地支”以“子”字开始，两者按干支顺序相配，其相配顺序为：甲子，乙丑，…，癸酉，甲戌，乙亥，…，壬戌，癸亥，甲子，…，周而复始，循环记录，此为干支纪年法．十三届全国人大四次会议审查的《国民经济和社会发展第十四个五年规划和2035年远景目标纲要（草案）》提出，展望2035年，中国将基本实现社会主义现代化．已知1901年是“干支纪年法”中的辛丑年，那么2035年是“干支纪年法”中的（　　）

A.．甲寅年

B.．乙卯年

C.丙辰年

D.丁巳年

解析

纠错

下载

相似

组卷

6. （本题5分）已知△ABC，则“sinA＞cosB”是“tanAtanB＞1”的（　　）

A.充分不必要条件	B.必要不充分条件
C.充分必要条件	D.既不充分也不必要条件

解析

纠错

下载

相似

组卷

7. （本题5分）已知某几何体的三视图如图所示，则该几何体的最长棱的长度为（　　）

B.．

C.．

解析

纠错

下载

相似

组卷

8. （本题5分） 2019年在阿塞拜疆举行的联合国教科文组织第43届世界遗产大会上，随着木槌落定，良渚古城遗址成功列入《世界遗产名录》，这座见证了中华五千多年文明史的古城迎来了在世界文明舞台上的“高光时刻”，标志着良渚是实证中华五千多年文明史的圣地，得到了世界的广泛认同.2010年，考古学家对良渚古城水利系统中一条水坝的建筑材料（草裹泥）上提取的草茎遗存进行碳14年代学检测，检查测出碳14的残留量约为初始值的55.2%，已知死亡生物体内碳14的含量y与生物死亡年数x之间符合

，其中k为死亡生物碳14的初始量．据此推断，此水坝大约是距2010年之前（　　）年建造的．
参考数据：lg552＝2.74，lg2＝0.30

A.．4912

B.4930

C.．4954

D.．4966

解析

纠错

下载

相似

组卷

9. （本题5分）（x﹣

+1）⁵展开式中的常数项为（　　）

A.1

B.．11

C.﹣19

D.51

解析

纠错

下载

相似

组卷

10. （本题5分）在△ABC中，角A，B，C对应的边分别是a，b，c，若3ccosA+acosC＝0，则B的最大值为（　　）

B.．

D.．

解析

纠错

下载

相似

组卷

11. （本题5分）已知双曲线

（a＞0，b＞0）的左、右焦点分别是F₁，F₂，在其渐近线上存在一点P，满足||PF₁|﹣|PF₂||＝2b，则该双曲线离心率的取值范围为（　　）

A.．（1，

）

B.（

，2）

C.．（

，

）

D.（2，3）

解析

纠错

下载

相似

组卷

12. （本题5分）若不等式e^x﹣aln（ax﹣1）+1≥0对∀x∈[

，1]恒成立（e为自然对数的底数），则实数a的最大值为（　　）

A.．e+1

B.e

C.．e²+1

D.．e²

解析

纠错

下载

相似

组卷

二、填空题(4小题共20分)

13. （本题5分）已知在△ABC中，AB＝2，AC＝1，D为BC的中点，则

＝　．

解析

纠错

下载

相似

组卷

14. （本题5分）曲线f（x）＝e^x+sinx（e为自然对数的底数）在x＝0处的切线与圆（x﹣2）²+y²＝9相交于点M，N，则|MN|＝　　．

解析

纠错

下载

相似

组卷

15. （本题5分）已知椭圆

的焦点为F₁，F₂，第一象限点P在C上，且

，则△PF₁F₂的内切圆半径为　

解析

纠错

下载

相似

组卷

16. （本题5分）如图，DE是边长为6的正三角形ABC的一条中位线，将△ADE沿直线DE翻折至△A₁DE，当三棱锥A₁﹣CED的体积最大时，四棱锥A₁﹣BCDE外接球O的表面积为　39π　；过EC的中点M作球O的截面，则所得截面圆面积的最小值是　．

解析

纠错

下载

相似

组卷

三、解答题(7小题共70分)

17. （本题12分）已知各项为正的数列{a_n}的首项a₁＝2，前n项和为S_n，且满足S_n+S_n_﹣1＝

（n≥2），数列{b_n}满足b₁＝1，3b_n₊₁＝b_n（n∈N^*）．
（1）求数列{a_n}和{b_n}的通项公式；
（2）若数列{c_n}满足c_n＝

•b_n，求{c_n}的前n项和T_n．

解析

纠错

下载

相似

组卷

18. （本题12分）已知三棱柱ABC﹣A₁B₁C₁，点O为棱AB的中点．
（Ⅰ）求证：BC₁∥平面A₁CO；
（Ⅱ）若△ABC是等边三角形，且AB＝AA₁，∠A₁AB＝60°，平面AA₁B₁B⊥平面ABC，求二面角A﹣A₁C﹣B的余弦值．

解析

纠错

下载

相似

组卷

19. （本题12分）新冠疫情在西方国家大流行，国际卫生组织对某国家进行新型冠状病毒感染率抽样调查．在某地抽取n人，每人一份血样，共n（n∈N^*）份，为快速有效地检验出感染过新型冠状病毒者，下面给出两种方案：
方案甲：逐份检验，需要检验n次；
方案乙：混合检验，把受检验者的血样分组，假设某组有k（k∈N^*，k≥2）份，分别从k份血样中取出一部分血液混合在一起检验，若检验结果为阴性，则说明这k个人全部为阴性，因而这k个人的血样只要检验这一次就够了；若检验结果为阳性，为了明确这k个人中究竟哪些人感染过新型冠状病毒，就要对这k个人的血样再逐份检验，因此这k个人的总检验次数就为k+1．
假设在接受检验的人中，每个人血样检验结果是阳性还是阴性是相互独立的，且每个人血样的检验结果是阳性的概率为p（0＜p＜1）．
（Ⅰ）若n＝5，p＝0.2，用甲方案进行检验，求5人中恰有2人感染过新型冠状病毒的概率；
（Ⅱ）记ξ为用方案乙对k个人的血样总共需要检验的次数．
①当k＝5，p＝0.2时，求E（ξ）；
②从统计学的角度分析，p在什么范围内取值，用方案乙能减少总检验次数？
（参考数据：0.8⁴＝0.41，0.8⁵＝0.33，0.8⁶＝0.26）

解析

纠错

下载

相似

组卷

20. （本题12分）已知函数f（x）＝e^x．
（1）若关于x的不等式f（x）≥a（sinx+cosx）在

上恒成立，求实数a的取值范围；
（2）当

时，证明：f（x）≥sinx+cosx．

解析

纠错

下载

相似

组卷

21. （本题12分）设抛物线C：x²＝2py（p＞0）的焦点为F，抛物线C上一点A的横坐标为x₁（x₁＞0），过点A作抛物线C的切线l₁，与x轴交于点D，与y轴交于点E，与直线l：

交于点M．当|FD|＝2时，∠AFD＝60°．
（1）求抛物线C的方程；
（2）若B为y轴左侧抛物线C上一点，过B作抛物线C的切线l₂，与直线l₁交于点P，与直线l交于点N，求△PMN面积的最小值，并求取到最小值时x₁的值．

解析

纠错

下载

相似

组卷

22. （本题10分）在直角坐标系xOy中，曲线C的参数方程为

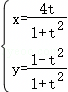（t为参数）．以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为ρcosθ﹣ρsinθ﹣4＝0．
（1）求C和l的直角坐标方程；
（2）若P为曲线C上任意一点，直线l与x轴、y轴的交点分别为A，B，求△PAB面积的最大值．

解析

纠错

下载

相似

组卷

23. （本题0分）．已知a，b，c都为正实数，且a+b+c＝3．证明：
（1）

；
（2）

．

解析

纠错

下载

相似

组卷

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

se@dyw.com

2022-04-07

高中数学 | 模考 | 难度:1.39

下载量
浏览量
收益额

下载试卷	收藏
平行组卷	细目重组
试卷分析	加入白板
加卷篮	更多功能

同类试卷 更多>>

2021年陕西省西安市西安中学高考数学二模试卷（理科）

更新:2021-03-18 12:07浏览量:546

2024-2025学年陕西省西安市高新一中高三（上）月考数学试卷（二模）

更新:2024-03-18 04:53浏览量:64

2024-2025学年陕西省西安市高新一中高三（上）第三次模拟数学试卷

更新:2024-04-04 06:23浏览量:35

2024-2025学年陕西省西安建筑科技大学附属中学高三（上）月考数学试卷（一模）

更新:2024-03-13 08:20浏览量:42

2024-2025学年陕西省西安八十五中高三（上）第一次模拟数学试卷

更新:2024-03-12 06:30浏览量:31

2024-2025年陕西省西安市高新一中高三（上）第五次模拟数学试卷

更新:2024-05-13 09:53浏览量:37

2023-2024学年陕西省西安市周至四中高三（上）月考数学试卷（理科）（一模）

更新:2023-03-04 02:06浏览量:37

2024年陕西师大附中高考数学十模试卷（理科）

更新:2024-07-09 05:34浏览量:34

2024年陕西省西安中学高考数学模拟试卷（文科）（一）

更新:2024-03-07 08:48浏览量:44

2024年陕西省西安中学高考数学模拟试卷（理科）（一）

更新:2024-03-11 01:46浏览量:37

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

微信扫码立即登录

AI助手

2022年陕西省西安市长安一中高考数学三模试卷（理科）

登录

注册

微信扫码立即登录

AI助手

2022年陕西省西安市长安一中高考数学三模试卷（理科）