服务热线
搜题▪组卷
 在一次函数的学习中,我们经历了“画出函数的图象——根据图象研究函数的性质——运用函数的性质解决问题”的学习过程,结合上面的学习过程,解决下面的问题:对于函数y=|x|+2.
在一次函数的学习中,我们经历了“画出函数的图象——根据图象研究函数的性质——运用函数的性质解决问题”的学习过程,结合上面的学习过程,解决下面的问题:对于函数y=|x|+2.| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | -6 | -4 | m | 0 | 2 | 0 | -2 | n | … |

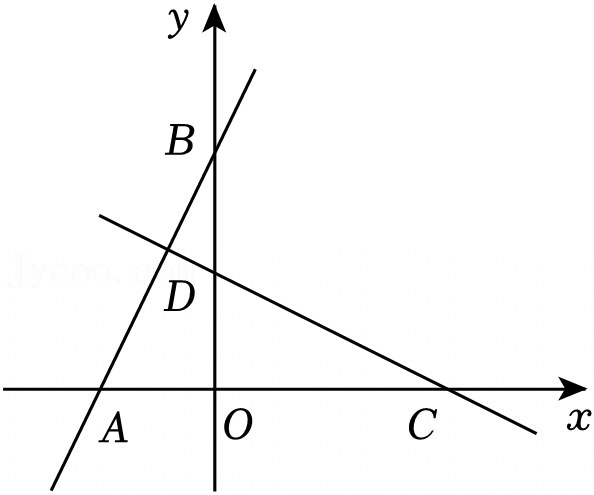
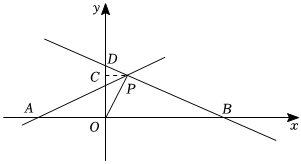 如图,A,B分别是x轴上位于原点左右两侧的两点,点P(2,p)在第一象限内,直线PA交y轴于点C(0,2),直线PB交y轴于点D,且S△AOP=6.
如图,A,B分别是x轴上位于原点左右两侧的两点,点P(2,p)在第一象限内,直线PA交y轴于点C(0,2),直线PB交y轴于点D,且S△AOP=6.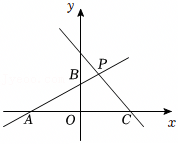
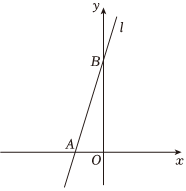 如图,在平面直角坐标系中,直线l交x轴于点A(-1,0)、交y轴于点B(0,3).
如图,在平面直角坐标系中,直线l交x轴于点A(-1,0)、交y轴于点B(0,3). 如图,在直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.点M(3,0)在x轴上,若点P是直线AB上的一个动点,当△PBM的面积与△AOB的面积相等时,求点P的坐标.
如图,在直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.点M(3,0)在x轴上,若点P是直线AB上的一个动点,当△PBM的面积与△AOB的面积相等时,求点P的坐标.
 已知一次函数y=2x+4.
已知一次函数y=2x+4.| x | 0 | 1 |
| y |
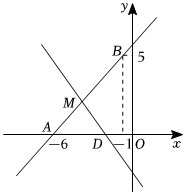 如图直线:y1=kx+b经过点A(-6,0),B(-1,5).
如图直线:y1=kx+b经过点A(-6,0),B(-1,5).

cb@dyw.com
2025-05-18
初中数学 | 八年级下 | 解答题