德优网2023陕西省西安市雁塔区师大附中高中数学模考模拟
2023年陕西师大附中高考数学第十一次模拟试卷(理科)
试卷总分:150分
命题人:dygzsxyn
考试时长:120分钟
一、选择题(12小题共60分)
1.
(本题5分)
已知集合A={x|ln(x﹣1)<0},B={y|y=2x﹣1,x∈A},则A∪B=( )
A.(1,2)
B..(1,3)
C..(﹣1,3)
D.(﹣1,+∞)
2.
(本题5分)
如果一个复数的实部和虚部相等,则称这个复数为“等部复数”,若复数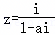 (i为虚数单位)为“等部复数”,则实数a的值为( )
(i为虚数单位)为“等部复数”,则实数a的值为( )
3.
(本题5分)
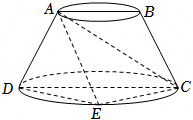
若圆锥的母线长为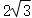 ,侧面展开图的面积为6π,则该圆锥的体积是( )
,侧面展开图的面积为6π,则该圆锥的体积是( )
A.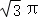
B.3π
C.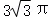
D.9π
4.
(本题5分)
我市拟向新疆哈密地区的三所中学派出5名教师支教,要求每所中学至少派遣一名教师,则不同的派出方法有( )
A.300种
B..150种
C..120种
D..90种
5.
(本题5分)
若(x﹣2)4(x2+3x)=a0+a1(x﹣2)+a2(x﹣2)2+⋯+an(x﹣2)n,则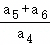 =( )
=( )
6.
(本题5分)
在如今这个5G时代,6G研究已方兴未艾.2021年8月30日第九届未来信息通信技术国际研讨会在北京举办.会上传出消息,未来6G速率有望达到1Tbps,并启用毫米波、太赫兹、可见光等尖端科技,有望打造出空天地融合的立体网络,预计6G数据传输速率有望比5G快100倍,时延达到亚毫秒级水平.香农公式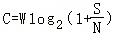 是被广泛公认的通信理论基础和研究依据,它表示:在受噪声干扰的信道中,最大信息传递率C取决于信道带宽W、信道内信号的平均功率S,信道内部的高斯噪声功率N的大小,其中
是被广泛公认的通信理论基础和研究依据,它表示:在受噪声干扰的信道中,最大信息传递率C取决于信道带宽W、信道内信号的平均功率S,信道内部的高斯噪声功率N的大小,其中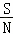 叫做信噪比.若不改变带宽W,而将信噪比
叫做信噪比.若不改变带宽W,而将信噪比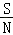 从11提升至499,则最大信息传递率C会提升到原来的( )参考数据:log23=1.58,log25=2.32.
从11提升至499,则最大信息传递率C会提升到原来的( )参考数据:log23=1.58,log25=2.32.
A.2.4倍
B.2.5倍
C..2.6倍
D..2.7倍
7.
(本题5分)
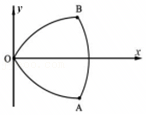
已知抛物线C:y2=2px(p>0),倾斜角为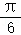 的直线交C于A,B两点,若线段AB中点的纵坐标为
的直线交C于A,B两点,若线段AB中点的纵坐标为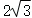 ,则p的值为( )
,则p的值为( )
A.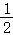
B..1
C..2
D.4
8.
(本题5分)
已知函数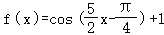 ,若将y=f(x)的图像向右平移m(m>0)个单位长度后图像关于y轴对称,则实数m的最小值为( )
,若将y=f(x)的图像向右平移m(m>0)个单位长度后图像关于y轴对称,则实数m的最小值为( )
9.
(本题5分)
已知函数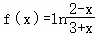 ,a=log23,b=log34,
,a=log23,b=log34,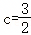 ,则( )
,则( )
|
A.f(a)<f(b)<f(c)
|
B..f(a)<f(c)<f(b)
|
|
C.f(c)<f(a)<f(b)
|
D.f(c)<f(b)<f(a)
|
10.
(本题5分)
已知双曲线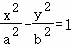 (a>0,b>0)的左、右焦点分别为F1,F2,过点F1且垂直于x轴的直线与该双曲线的左支交于A,B两点,若△ABF2的周长为16,则当b2取得最大值时,该双曲线的离心率为( )
(a>0,b>0)的左、右焦点分别为F1,F2,过点F1且垂直于x轴的直线与该双曲线的左支交于A,B两点,若△ABF2的周长为16,则当b2取得最大值时,该双曲线的离心率为( )
11.
(本题5分)
已知函数f(x),g(x)的定义域均为R,f(x)为偶函数且f(x)+f(x+2)=3,g(x)+g(10﹣x)=2,则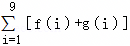 =( )
=( )
A.21
B.22
C.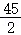
D.
12.
(本题5分)
已知函数f(x)=lnx+1﹣mx2有两个零点a,b,且存在唯一的整数x0∈[a,b],则实数m的取值范围为( )
转载声明:
本题解析属于发布者收集录入,如涉及版权请向平台申诉!
!版权申诉