服务热线
搜题▪组卷
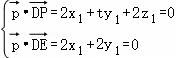 ,取x1=2,得
,取x1=2,得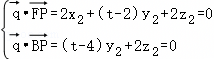 ,取x2=2,得
,取x2=2,得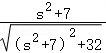 ,设s2+7=r,则y=
,设s2+7=r,则y=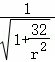 ,
,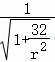 在r∈[7,16)时递增,
在r∈[7,16)时递增,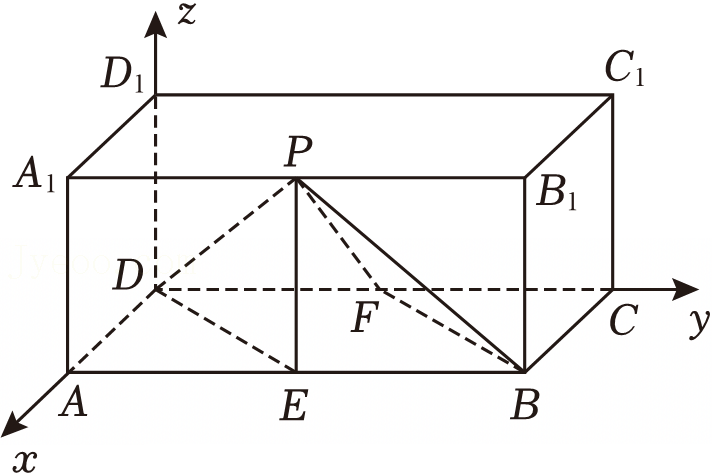
A.直线A1C1与直线BD所成角为90°
B..直线A1C1与平面A1BD所成角的正弦值为![]()
C.二面角C1﹣A1B﹣D的余弦值为![]()
D..如果AB=1,那么点C1到平面A1BD的距离为![]()
A.若k1+k2=2,则M的轨迹是椭圆(除去两个点)
B.若k1﹣k2=2,则M的轨迹是抛物线(除去两个点)
C..若k1•k2=2,则M的轨迹是双曲线(除去两个点)
D.若k1÷k2=2,则M的轨迹是一条直线(除去一点)
A.1不是函数f(x)=x+![]() (x>0)的一个下界
(x>0)的一个下界
B..函数f(x)=xlnx有下界,无上界
C.函数f(x)=![]() 有上界,无下界
有上界,无下界
D.函数f(x)=![]() 有界
有界
A.设A,B是两定点,k为非零常数,若|![]() |﹣|
|﹣|![]() |=k,则动点P的轨迹为双曲线的一支
|=k,则动点P的轨迹为双曲线的一支
B.过定圆C上一定点A作圆的动弦AB,O为坐标原点,若![]() =
=![]() (
(![]()
![]() ),则动点P的轨迹为椭圆
),则动点P的轨迹为椭圆
C.方程2x2﹣5x+2=0的两根可分别作为椭圆和双曲线的离心率
D.双曲线![]()
![]() =1与椭圆x2
=1与椭圆x2![]() =1有相同的焦点
=1有相同的焦点
A.若b2+c2﹣a2>0,则△ABC为锐角三角形
B.若A>B,则sinA>sinB
C.若b=3,A=60°,三角形面积S=3![]() ,则a=
,则a=![]()
D..若acosA=bcosB,则△ABC为等腰三角形
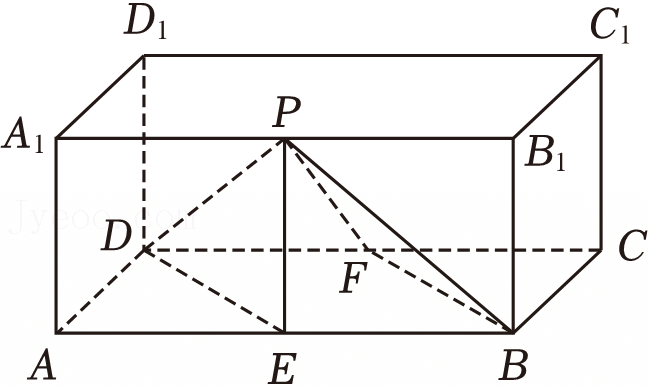
A.存在唯一点P,使得D1P⊥B1C
B.当点P在AC上移动时,直线D1P与直线B1D所成角不变
C.直线D1P与平面ABCD所成角的最小值为![]()
D..当D1P=3时,点P的轨迹为圆的一部分
A.直线A1G,C1E为异面直线
B.直线A1G与平面DD1C1C所成角的正切值为![]()
C..过点C1,E,F的平面截正方体的截面面积为![]()
D.三棱锥B﹣AEF外接球的表面积为14π
A..PB⊥AC
B..异面直线DE和AB所成角的余弦值是![]()
C..AM+MB的最小值是4![]()
D..三棱锥P﹣ABC内切球的半径是![]()
A.若直线a不平行于平面α,a⊄α,则α内不存在与a平行的直线
B.若一个平面α内两条不平行的直线都平行于另一个平面β,则α∥β
C.设l,m,n为直线,m,n在平面α内,则“l⊥α”是“l⊥m且l⊥n”的充要条件
D..若平面α⊥平面α1,平面β⊥平面β1,则平面α与平面β所成的二面角和平面α1与平面β1所成的二面角相等或互补
A.直线DC1与BC所成角为90°
B.三棱锥D﹣BCC1的体积为![]()
C.二面角A1﹣BD﹣C1的大小为60°
D..直三棱柱ABC﹣A1B1C1外接球的表面积为6π
A.x>2且y>3是x+y>5的充要条件
B.“x>1”是“|x|>0”的充分不必要条件
C..b2﹣4ac=0是ax2+bx+c=0(a≠0)有实数解的充要条件
D..三角形的三边满足勾股定理的充要条件是此三角形为直角三角形
A.若![]() 则O为△ABC的重心
则O为△ABC的重心
B.若![]() ,则点O为△ABC的垂心
,则点O为△ABC的垂心
C..在△ABC中,向量![]() 与
与![]() 满足
满足![]() ,且
,且![]() ,则△ABC为等边三角形
,则△ABC为等边三角形
D.若![]() ,S△AOC,S△ABC分别表示△AOC,△ABC的面积,则S△AOC:S△ABC=1:6
,S△AOC,S△ABC分别表示△AOC,△ABC的面积,则S△AOC:S△ABC=1:6
A.三棱锥D′﹣ABC的外接球表面积为32π
B.直线MN与平面ABC所成角的正切值为![]()
C..点C到平面OMN的距离为![]()
D.三角形MON沿直线MN旋转一周得到的旋转体的体积为![]()
A.直线l的倾斜角是π﹣α
B.无论α取何值,直线l与圆x2+y2=1相切
C..直线l的斜率一定存在
D..当直线l和两坐标轴都相交时,它和坐标轴围成的三角形的面积不小于1

gr@dyw.com
2024-12-24
高中数学 | 高二上 | 多选题