微信扫码立即登录

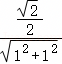A.．三棱锥P﹣ABC的体积为

B.直线PA与直线BC所成角的余弦值为 

C.直线PA与平面PBC所成角的正弦值为 

D.三棱锥P﹣ABC外接球的半径为

A.被截正方体的棱长为2 

B.．被截去的一个四面体的体积为  

C.．该二十四等边体的体积为 

D.该二十四等边体外接球的表面积为8π

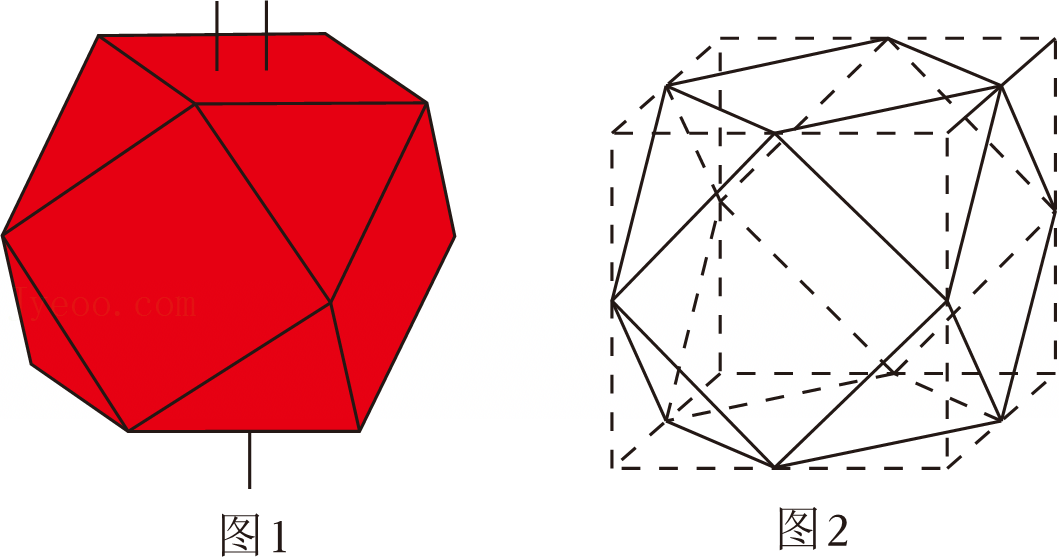
A.棱长为

B.两条棱所在直线异面时，这两条异面直线所成角的大小是60°  

C.表面积为  

D.外接球的体积为

A.直线A₁G，C₁E为异面直线  

B.直线A₁G与平面DD₁C₁C所成角的正切值为

C.．过点C₁，E，F的平面截正方体的截面面积为  

D.三棱锥B﹣AEF外接球的表面积为14π

A.直线A₁C₁与直线BD所成角为90°   

B.．直线A₁C₁与平面A₁BD所成角的正弦值为

C.二面角C₁﹣A₁B﹣D的余弦值为

D.．如果AB＝1，那么点C₁到平面A₁BD的距离为

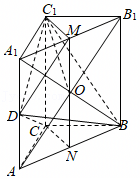
A.当|MN|最大时，MN与BC所成的角为 

B.三棱锥A₁﹣BNC₁的体积为定值

C.若|DN|＝2，则点N的轨迹长度为2π

D.若N∈平面A₁BCD₁，则BN+NC₁的最小值为

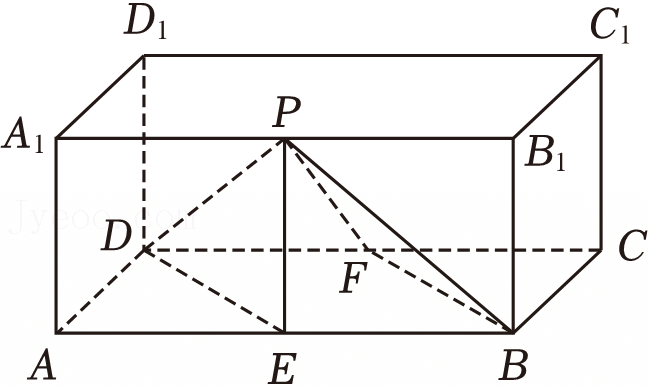
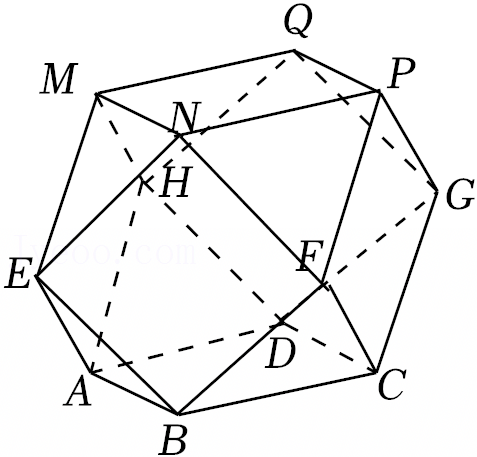
A.存在点P，使直线PE与平面PDF所成角取得最大值

B.存在点P，使直线PD与平面PEB所成角取得最大值

C.存在点P，使平面PDE与平面PFB的夹角取得最大值   

D.存在点P，使平面PDF与平面PEB的夹角取得最大值

A.点P的轨迹中包含AA₁的中点   

B.点P在侧面AA₁D₁D内的轨迹的长为 

C.MP长度的最大值为  

D.直线CC₁与直线MP所成角的余弦值的最大值为

A.AB₁⊥A₁M 

B.异面直线A₁B与B₁M所成角的取值范围为  

C.|A₁M|+|C₁M|的最小值为  

D.当M是BC的中点时，二面角A﹣A₁B₁﹣M的余弦值为

A.存在唯一点P，使得D₁P⊥B₁C   

B.当点P在AC上移动时，直线D₁P与直线B₁D所成角不变

C.直线D₁P与平面ABCD所成角的最小值为  

D.．当D₁P＝3时，点P的轨迹为圆的一部分

A.．三棱锥Q﹣C₁BD的体积为定值 

B.当点Q为B₁D₁中点时，直线QA₁与平面A₁BD所成角的正弦值为   

C.．当点Q与D₁重合时，三棱锥Q﹣A₁BD的外接球的体积为4

D.．过点Q平行于平面C₁BD的平面被正方体ABCD﹣A₁B₁C₁D₁截得的多边形的面积为2

A.EF∥A₁C₁ 

B.三棱锥E﹣A₁B₁F的体积为   

C.异面直线B₁E与A₁F所成角的余弦值为 

D.点E到直线B₁D₁的距离为

A.  

B.．   

C.．异面直线OD₁与EF所成角的余弦值为 

D.．点F到直线OD₁的距度为

A.．OM⊥AP

B.存在点M，使OM∥平面SBC 

C.．存在点M，使直线OM与AB所成的角为30°

D.．点M到平面ABCD与平面SAB的距离和为定值

A.若E是直线AC上的动点，则D₁E∥平面A₁BC₁ 

B.若E是直线BD₁上的动点，F是直线BD上的动点，则EF⊥AC

C.．若E是△ABC内（包括边界）的动点，则直线D₁E与平面ABC所成角的正切值的取值范围是 

D.若E是平面BA₁C₁内的动点，则三棱锥D₁﹣AEC的体积为定值