首页 > 试卷详情

德优网2025陕西省西安市雁塔区西安八十五中初中数学考试期中七年级下

2024-2025学年陕西省西安八十五中七年级（下）期中数学试卷

试卷总分:120分命题人:dyczsxyn 考试时长:120分钟

一、选择题(8小题共24分)

1. （本题3分）计算（-3）⁰的结果是（　　）

A.-3

B.-1

D.1

解析

纠错

下载

相似

组卷

2. （本题3分）剪纸是一种艺术创作，图案多以花鸟虫鱼、飞禽走兽等为表现对象．剪纸纸张的厚度通常可以达到0.0001m甚至更薄．将数据0.0001用科学记数法表示为（　　）

A.0.1×10⁴

B.1×10^-5

C.1×10^-4

D.1×10^-3

解析

纠错

下载

相似

组卷

3. （本题3分）如图，直线a∥b,∠1=50°，则∠2的度数为（　　）
$德优题库$

A.130°

B.110°

C.120°

D.150°

解析

纠错

下载

相似

组卷

4. （本题3分）计算（-3xy²）²的结果正确的是（　　）

A.3x²y²

B.9x²y⁴

C.6x²y⁴

D.6xy²

解析

纠错

下载

相似

组卷

5. （本题3分）下列事件为随机事件的是（　　）

A.胡老师打开微信时恰好有一条未读信息

B.自然状态下的水从低处向高处流

C.明天太阳从东方升起

D.地球绕太阳转

解析

纠错

下载

相似

组卷

6. （本题3分）若y（y-8）+a=（y-4）²，则a的值是（　　）

A.8

B.16

C.32

D.64

解析

纠错

下载

相似

组卷

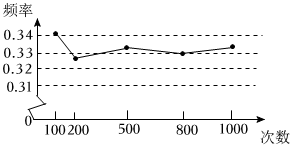7. （本题3分） $德优题库$ 某小组做“用频率估计概率”的试验时，统计了某一事件发生的频率，绘制了如图所示的折线图．该事件最有可能的是（　　）

A.掷一个质地均匀的正六面骰子，向上一面的点数是2

B.从一副扑克牌中任意抽取1张，这张牌是“红心”

C.暗箱中有1个红球和2个黄球，这些球除了颜色外无其它差别，从中任取一球是红球

D.掷一枚硬币，正面朝上

解析

纠错

下载

相似

组卷

8. （本题3分） $德优题库$ 如图，在△ABC中，∠BAC=90°，且AD，AE，BF分别是△ABC的高线，中线和角平分线，且AD与BF相交于点G，下列结论不一定正确的是（　　）

A.∠BAD=∠C	B.∠AGF=∠AFG
C.S_△ABE=S_△AEC	D.AC-AE＜DE

解析

纠错

下载

相似

组卷

二、填空题(5小题共15分)

9. （本题3分）若长度分别为3，5，x的三条线段能组成一个三角形，则x的值可以是．（写出一个符合题意的数即可）

解析

纠错

下载

相似

组卷

10. （本题3分） $德优题库$ 如图，△ABC中，ED∥AC，∠B=55°，∠DEB=90°，则∠A的度数为．

解析

纠错

下载

相似

组卷

11. （本题3分） $德优题库$ 如图，一个转盘被分成3个扇形，扇形A、扇形B、扇形C的圆心角分别为90°，120°，150°，自由转动转盘1次，则指针落在扇形A的概率是．

解析

纠错

下载

相似

组卷

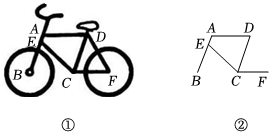12. （本题3分） $德优题库$ 健康骑行越来越受到大家的喜欢，如图①是某自行车车架的实物图，图②是其部分平面示意图，已知AB∥CD，AD∥CF，点E在AB上，∠BEC=67°，∠ADC=70°，则∠ECF的度数为．

解析

纠错

下载

相似

组卷

13. （本题3分）有两个正方形A，B，现将B放在A的内部如图1，将A，B并排放置后构造新的正方形如图2，若图1和图2中阴影部分的面积分别为

和

，则正方形A，B的面积之和为　　．

解析

纠错

下载

相似

组卷

三、解答题(13小题共81分)

14. （本题5分）计算：a²•a⁴+（-2a²）³+a⁸÷a²．

解析

纠错

下载

相似

组卷

15. （本题5分）计算：（2x+5y-1）（2x+5y+1）．

解析

纠错

下载

相似

组卷

16. （本题5分）计算：

．

解析

纠错

下载

相似

组卷

17. （本题5分） $德优题库$ 如图，点B是∠DAC的边AC上一点，请用尺规作图法，过点B作射线AD的平行线．（保留作图痕迹，不写作法）

解析

纠错

下载

相似

组卷

18. （本题5分） $德优题库$ 如图，点D，E，F分别是△ABC的边BC，CA，AB上的点，DF∥CA，∠FDE=∠A．求证：DE∥AB．

解析

纠错

下载

相似

组卷

19. （本题5分）一个不透明的口袋中装有6个白球和10个红球，4个黄球，每个球除颜色外都相同．从口袋中任意摸出一个球．
（1）P（摸到红球）= ；
（2）P（摸到不是白球）= ；
（3）从口袋中取走x个红球，使摸到红球和白球的概率相等，求x的值．

解析

纠错

下载

相似

组卷

20. （本题5分） $德优题库$ 如图，直线CD，EF相交于点O，OA⊥OB，若∠AOE=57°，∠COF=86°，求∠BOD的度数．

解析

纠错

下载

相似

组卷

21. （本题6分）先化简，再求值：（n+m）（m﹣n）﹣（4m³n﹣2mn³）÷2mn，其中

．

解析

纠错

下载

相似

组卷

22. （本题7分）小丽和小亮用10张写有1～10的卡片做游戏，这10张卡片除数字外完全相同，将它们背面朝上混合均匀后，从中任意抽出一张．
（1）抽出卡片上的数字是3的倍数的概率是；
（2）小丽和小亮规定：小丽从中任意抽出一张卡片，小亮从剩余的卡片中任意抽出一张，谁抽到卡片上的数字大谁就获胜，现在小丽抽到数字6的卡片，然后小亮抽出卡片，那么谁获胜的概率大？

解析

纠错

下载

相似

组卷

23. （本题7分）已知a^m=5，aⁿ=3．
（1）求a^m-n的值；
（2）求a^1+2m•a^3n-1的值．

解析

纠错

下载

相似

组卷

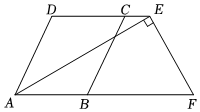24. （本题8分） $德优题库$ 如图，AD∥BC，∠DCB=∠DAB，点E，F分别在直线DC，AB上，AE⊥EF．
（1）DC与AB平行吗？请说明理由；
（2）若∠DAE=∠DEA，∠DAB=60°，求∠F的度数．

解析

纠错

下载

相似

组卷

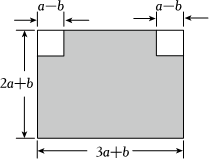25. （本题8分） $德优题库$ 如图，和谐广场有一块长为（3a+b）米，宽为（2a+b）米的长方形土地，现要将阴影部分进行绿化，在上方两角处留两块边长为（a-b）米的小正方形空地．
（1）用含有a,b的式子表示绿化部分的总面积；（结果写成最简形式）
（2）若a=40，b=20，求出绿化部分的总面积．

解析

纠错

下载

相似

组卷

26. （本题10分）【问题提出】
（1）如图①，AB∥CD，∠D=15°，∠GAB=70°，求∠P的度数；
（2）如图②，AB∥CD，点E在直线CD上，点P在直线AB上方，连接PA，PE，请写出∠PAB，∠CEP，∠APE之间的数量关系，并说明理由；
【拓展延伸】
（3）如图③，AB∥CD，点E在直线CD上，点P在直线AB上方，连接PA，PE，∠PED的平分线EQ与∠PAB的平分线AF所在直线交于点Q，求2∠AQE+∠APE的值．
$德优题库$

解析

纠错

下载

相似

组卷

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

dyczsxyn

2025-05-14

初中数学 | 考试 | 难度:1.46

下载量
浏览量
收益额

同类试卷 更多>>

2021-2022学年陕西省西安市铁一中学九上数学期中试卷

更新:2021-11-15 02:44浏览量:1046

2021-2022学年陕西省西安市高新一中八上数学期中试卷

更新:2021-11-18 08:40浏览量:1011

2021-2022学年陕西省西安市铁一中学七上数学期中试卷

更新:2021-11-22 10:21浏览量:1197

2021-2022学年陕西省西安市铁一中学八上数学期中试卷

更新:2021-11-19 01:05浏览量:1107

2021-2022学年陕西省西安市高新一中九上数学期中试卷

更新:2021-11-25 06:43浏览量:952

2021-2022学年陕西省西安市西工大附中八上数学期中试卷

更新:2021-11-19 03:19浏览量:1138

2021-2022学年陕西省西安市交大附中八上数学期中试卷

更新:2021-11-27 03:51浏览量:1163

2021-2022学年陕西省西安市交大附中七上数学期中试卷

更新:2021-11-24 01:18浏览量:1155

2021-2022学年陕西省西安市师大附中七上数学期中试卷

更新:2021-11-23 03:34浏览量:1106

2021-2022学年陕西省西安市交大附中九上数学期中试卷

更新:2021-11-22 05:30浏览量:1015

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

普通登录

手机登录

微信扫码立即登录

2024-2025学年陕西省西安八十五中七年级（下）期中数学试卷