首页 > 试卷详情

德优网2024陕西省西安市高新区高新二中初中数学段考月考七年级下

2023-2024学年陕西省西安市雁塔区高新二中七年级（下）第一次月考数学试卷

试卷总分:120分命题人:dyczsxyn 考试时长:120分钟

一、选择题(8小题共24分)

1. （本题3分）计算m³•m²的结果，正确的是（　　）

A.m²

B.m³

C.m⁵

D.m⁶

解析

纠错

下载

相似

组卷

2. （本题3分） $德优题库$ 如图，直线AB与CD相交于点O，∠AOC=66°，则∠BOD的度数是（　　）

A.55°

B.66°

C.77°

D.88°

解析

纠错

下载

相似

组卷

3. （本题3分）为打造“比、学、赶、帮、超”良好的班风和浓厚的学风，数学白老师为8班孩子购买了5包卡通橡皮和x包表扬信，卡通橡皮每包12元，表扬信每包30元，共花费y元，则关系式为（　　）

A.y=5x+6

B.y=12x+30

C.y=8x+12

D.y=30x+60

解析

纠错

下载

相似

组卷

4. （本题3分）若2×8^m×16^m=2²⁹，则m的值是（　　）

A.3

B.4

C.5

D.6

解析

纠错

下载

相似

组卷

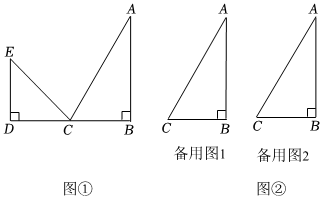
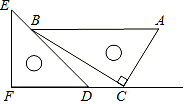5. （本题3分） $德优题库$ 一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，则∠DBC的度数为（　　）

A.10°

B.15°

C.18°

D.30°

解析

纠错

下载

相似

组卷

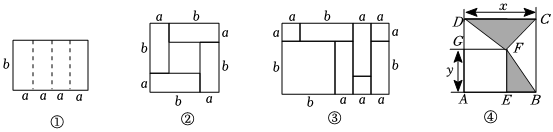
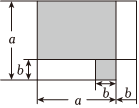6. （本题3分） $德优题库$ 如图，将一个边长为a的正方形，剪掉一个边长为b的小正方形后，剩余的部分可以拼成一个长方形，此操作过程能验证的等式是（　　）

A.（a+b）（a-b）=a²-b²	B.（a-b）²=a²-2ab+b²
C.（a+b）²=a²+2ab+b²	D.（a+b）（a-b）=a²+b²

解析

纠错

下载

相似

组卷

7. （本题3分）若（x-100）²+（x-102）²=6，则（x-101）²的值为（　　）

B.2

C.4

D.6

解析

纠错

下载

相似

组卷

8. （本题3分）已知：2^a=24，2^b=6，2^c=9，则下列结论：①a-b=2；②3b=a+c；③2b-c=2，其中不正确的个数是（　　）

A.0个

B.1个

C.2个

D.3个

解析

纠错

下载

相似

组卷

二、填空题(5小题共15分)

9. （本题3分） “练练峰上雪，芊芊云表霓”，这是杜甫眼中的雪，单个雪花的重量只有0.00003kg左右，数据“0.00003”用科学记数法表示为．

解析

纠错

下载

相似

组卷

10. （本题3分）一个角的余角的3倍比这个角的补角少12°，则这个角的度数为．

解析

纠错

下载

相似

组卷

11. （本题3分）某商店在开学季，书包薄利多销的促销活动．原价为560元，随着不同幅度的降价，日销量（单位：件）发生相应的变化：从表中可以看出，每降价5元，日销量增加件．

降价（元）	5	10	15	20	25	30	35
日销量（件）	780	810	840	870	900	930	960

解析

纠错

下载

相似

组卷

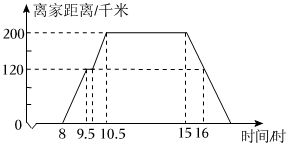12. （本题3分） $德优题库$ “唐时良辰，潮启长安”，西安新晋开放的“长安十二时辰”主题街区是宝藏唐风游玩打卡地．一个周末上午8：00，网红张斌自驾小汽车从家出发，带全家人去“长安十二时辰”游玩，在去“长安十二时辰”主题街区的路上，汽车加油用了12分钟，张斌驾驶的小汽车离家的距离y（千米）与时间t（时）之间的关系如图所示：
①张斌家距离距离“长安十二时辰”主题街区120千米；
②张斌一家人在“长安十二时辰”主题街区游玩了5.5小时；
③张斌一家返回到家的时间恰好是17时20分；
④汽车加油前的速度是80千米/时；正确的是．

解析

纠错

下载

相似

组卷

13. （本题3分） $德优题库$ 高速公路上安装如图①所示的激光灯可以预防司机疲劳驾驶，图②是激光为于初始位置时的平面几何示意图，其中C、D是直线AB上的两个发射点，∠ACE=60°，∠CDF=150°，现激光EC绕点C以2°/s的速度顺时针转动，同时激光FD绕点D以3°/s的速度逆时针转动，若转动t s后，激光EC与FD首次平行，则转动时间t应为 s.

解析

纠错

下载

相似

组卷

三、解答题(13小题共81分)

14. （本题6分）用乘法公式计算：2023²-2022×2024．

解析

纠错

下载

相似

组卷

15. （本题6分） $德优题库$ 如图，已知△ABC，点D在CA的延长线上，在射线AD上求作一点P，使得∠PBC=2∠ABC．（保留作图痕迹，不写作法）

解析

纠错

下载

相似

组卷

16. （本题6分）已知计算（5-3x+mx²-6x³）•（-2x²）-x（-3x³+nx-1）的结果中不含x⁴和x²的项，求m、n的值．

解析

纠错

下载

相似

组卷

17. （本题6分） $德优题库$ 已知O为直线AB上一点，∠COE=90°，OF平分∠AOE．若∠COF=35°，求∠AOC、∠BOE的度数．

解析

纠错

下载

相似

组卷

18. （本题6分）先化简，再求值．
（2x-3y）²-（x-2y）（x-5y）-（2x+y）（2x-y），其中x=-1，y=2．

解析

纠错

下载

相似

组卷

19. （本题6分）两条直线被第三条直线所截，∠1和∠2是同旁内角，∠3和∠2是内错角．
（1）根据上述条件，画出符合题意的示意图；
（2）若∠1=3∠2、∠2=3∠3，求∠1，∠2的度数．

解析

纠错

下载

相似

组卷

20. （本题6分）一辆汽车油箱内有油56升，从某地出发，每行驶1千米，耗油0.08升，如果设油箱内剩油量为y（升），行驶路程为x（千米），则y随x的变化而变化．
（1）写出y与x的关系式．
（2）这辆汽车行驶350千米时剩油多少升？汽车剩油8升时，行驶了多少千米？

解析

纠错

下载

相似

组卷

21. （本题6分）如图所示的是人民公园的一块长为（2m+n）米．宽为（m+2n）米的空地．预计在空地上建造一个网红打卡观景台（阴影部分）．
$德优题库$
（1）请用m、n表示观景台的面积．（结果化为最简）
（2）如果修建观景台的费用为200元/平方米．且已知m=5（米），n=4（米）．那么修建观景台需要费用多少元？

解析

纠错

下载

相似

组卷

22. （本题6分）将一副三角板中的两块直角三角尺顶点C按照如图①方式叠放在一起（其中∠ABC=∠CDE=90°，∠ACB=60°，∠A=30°，∠E=∠ECD=45°），设∠ACE=α．将三角形CDE绕点C顺时针转动，若DE∥BC，求α的度数．
$德优题库$

解析

纠错

下载

相似

组卷

23. （本题6分）若x满足（9-x）（x-4）=4，求（9-x）²+（x-4）²的值．
解：设9-x=a,x-4=b,则ab=（9-x）（x-4）=4，a+b=（9-x）+（x-4）=5，
所以（a+b）²=a²+2ab+b²=a²+8+b²=25，
所以a²+b²=17，即（9-x）²+（x-4）²=17．
请仿照上面的方法求解下面问题：
（1）若x满足（5-x）（x-2）=2，求代数式（5-x）²+（x-2）²的值；
（2）若x满足（6-x）（4-x）=8，求代数式（10-2x）²的值．

解析

纠错

下载

相似

组卷

24. （本题6分）为保护学生的视力，课桌椅的高度均按一定的关系配套设计．已知课桌的高度随着椅子的高度变化而变化，它们之间的关系可近似地表示为y=1.6x+11，其中y表示课桌的高度（单位：cm），x表示椅子的高度（单位：cm）．
（1）求当椅子的高度为40cm时，课桌的高度．
（2）求当课桌的高度为83cm时，椅子的高度．

解析

纠错

下载

相似

组卷

25. （本题6分）如图①是一个长为4a、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图②）．
（1）根据上述过程，写出（a+b）²、（a-b）²、ab之间的等量关系：       ；
（2）利用（1）中的结论，若x+y=4，xy=1，则（x-y）²的值是        ；
（3）实际上通过计算图形的面积可以探求相应的等式，如图③，请你写出这个等式：       ；
（4）两个正方形ABCD，AEFG如图④摆放，边长分别为x,y,若x²+y²=34，BE=2，求图中阴影部分面积和．
$德优题库$

解析

纠错

下载

相似

组卷

26. （本题9分）学习了平行线的判定与性质后，某兴趣小组在练习中看到这样一道题“如图1，AP平分∠BAC，CP平分∠ACD，∠1+∠2=90°．判断AB，CD是否平行，并说明理由”，试着“玩”起数学来：
【基础巩固】
（1）条件和结论互换，改成了：“如图1，AP平分∠BAC，CP平分∠ACD，AB∥CD，则∠1+∠2=90°．”小明认为这个结论正确，你认同他的想法吗？请说明理由．
【尝试探究】
（2）小明发现：若将其中一条角平分线改成AC的垂线，则“∠1+∠2=90°”这个结论不成立．请帮小明完成探究：
如图2，AB∥CD，AP平分∠BAC，CP⊥AC，∠1是AP与AB的夹角，∠2是CP与CD的夹角，若∠2=22°，求∠1的度数．
【拓展提高】
（3）如图3，若AB∥CD，AP⊥AC，CP平分∠ACD，试说明∠1+2∠2=90°．
$德优题库$

解析

纠错

下载

相似

组卷

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

wy@dyw.com

2024-04-25

初中数学 | 段考 | 难度:1.65

下载量
浏览量
收益额

下载试卷	收藏
平行组卷	细目重组
试卷分析	加入白板
加卷篮	更多功能

同类试卷 更多>>

2021届陕西省西安市铁一中学八上数学第一次月考试卷

更新:2020-10-13 01:00浏览量:1229

2022届陕西省西安市师大附中九上数学第一次月考试卷

更新:2021-10-15 06:59浏览量:1125

2020-2021学年陕西省西安市铁一中学八上数学第二次月考试卷

更新:2021-12-15 07:40浏览量:1155

2020-2021学年陕西省西安市西工大附中八上数学第二次月考试卷

更新:2021-01-09 06:11浏览量:905

2024-2025学年陕西省西安市铁一中学七年级（上）第一次月考数学试卷

更新:2024-10-21 10:43浏览量:67

2023-2024学年陕西省西安市雁塔区高新一中七年级（上）第二次月考数学试卷

更新:2023-12-16 05:47浏览量:588

2023-2024学年陕西省西安市爱知中学八年级（上）第一次月考数学试卷

更新:2023-10-18 05:48浏览量:722

2023-2024学年陕西省西安交大附中航天学校九年级（上）第二次月考数学试卷

更新:2023-10-10 05:49浏览量:578

2023-2024学年陕西省西安市汇知中学七下第一次月考数学试卷

更新:2024-04-25 07:12浏览量:655

2024-2025学年陕西师大附中七年级（上）月考数学试卷（10月份）

更新:2024-10-22 01:41浏览量:143

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

微信扫码立即登录

AI助手

2023-2024学年陕西省西安市雁塔区高新二中七年级（下）第一次月考数学试卷

登录

注册

微信扫码立即登录

AI助手

2023-2024学年陕西省西安市雁塔区高新二中七年级（下）第一次月考数学试卷