服务热线
搜题▪组卷
试卷总分:120分 命题人:dyczsxyn 考试时长:120分钟
A.当AC=BD时，四边形ABCD是矩形
B.当AB=AD，CB=CD时，四边形ABCD是菱形
C.当AB=AD=BC时，四边形ABCD是菱形
D.当AC=BD，AD=AB时，四边形ABCD是正方形
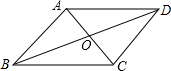如图，在四边形ABCD中，对角线AC、BD互相平分，若添加一个条件使得四边形ABCD是菱形，则这个条件可以是（ ）
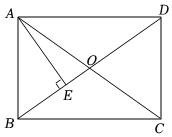如图，矩形ABCD的对角线AC，BD相交于点O，AE⊥BD于点E，∠ADB=35°，则∠OAE的度数为（ ）
A.50（1+x）2=182
B.50+50（1+x）+50（1+x）2=182
C.50（1+2x）=182
D.50+50（1+x）+50（1+2x）=182
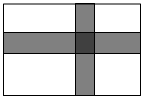如图，在一块长13m,宽7m的矩形空地上，修建同样宽的两条互相垂直的道路（两条道路分别与矩形的一条边平行），剩余部分栽种花草，若栽种花草的面积是72m2，则道路的宽应设计为多少m？
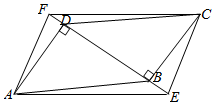如图，在▱ABCD中，将对角线BD分别向两个方向延长至点E、F，且BE=DF．连接AF、CF、CE、AE．
sel@dyw.com
2024-10-27
初中数学 | 段考 | 难度:2.15
| 下载试卷 | 收藏 |
| 平行组卷 | 细目重组 |
| 试卷分析 | 加入白板 |
| 加卷篮 | 更多功能 |
平行组卷卷生成中,请等待
解析
纠错
收藏
下载
相似
组卷
如图，在平行四边形ABCD中，E，F分别为边AB、CD的中点，BD是对角线，AG∥BD，且AG=BD，交CB的延长线于点G，连接FG，若AD⊥BD，下列结论：①DF∥BE；②四边形ADBG是矩形；③FG=AB；④4S△BFC=S▱ABCD，正确的有（ ）
如图，周长为16菱形ABCD的对角线相交于点O，E为AB的中点，连接OE．则OE的长为 ．
如图，P是矩形ABCD内的任意一点，连接PA，PB，PC，PD，得到△PAB，△PBC，△PCD，△PDA，设它们的面积分别是S1，S2，S3，S4．给出以下结论：①S1+S4=S2+S3；②S2+S4=S1+S3；③若S3=2S1，则S4=2S2，其中正确结论的序号是 ．
如图，已知在矩形ABCD中，请用尺规作图，分别在AD，BC上作点E，F，使四边形BEDF是菱形．（保留作图痕迹，不写作法）
如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．
如图，在矩形ABCD中，AB=8cm,BC=16cm,点P从点D出发向点A运动，运动到点A停止，同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s.连接PQ、AQ、CP．设点P、Q运动的时间为t s.