如图在中若的半径为点在上点在上连接求线段的最小值如图所示五边形是某市工业新区的外环路新区管委会在点处点处是该市的一个交通枢纽已知根据新区的自然环境及实际需求现要在矩形区域内含边界修一个半径为的圆型环道过圆心作垂足为与交于点连接点在

首页 > 试题列表 > 单题解析

25685. （2023•陕西省•真题）（1）如图①，在△OAB中，OA=OB，∠AOB=120°，AB=24．若⊙O的半径为4，点P在⊙O上，点M在AB上，连接PM，求线段PM的最小值；
（2）如图②所示，五边形ABCDE是某市工业新区的外环路，新区管委会在点B处，点E处是该市的一个交通枢纽．已知：∠A=∠ABC=∠AED=90°，AB=AE=10000m,BC=DE=6000m.根据新区的自然环境及实际需求，现要在矩形AFDE区域内（含边界）修一个半径为30m的圆型环道⊙O；过圆心O，作OM⊥AB，垂足为M，与⊙O交于点N．连接BN，点P在⊙O上，连接EP．其中，线段BN、EP及MN是要修的三条道路，要在所修道路BN、EP之和最短的情况下，使所修道路MN最短，试求此时环道⊙O的圆心O到AB的距离OM的长．
$德优题库$

共享时间:2023-07-20 难度:3

纠错

下载

相似

组卷

[考点]

等腰三角形的判定与性质，相似三角形的判定与性质，解直角三角形，切线的判定与性质，圆的综合题，

[答案]

（1）4-4；
（2）4047.91m．

[解析]

解：（1）如图①，连接OP，OM，过点O作OM'⊥AB，垂足为M'，
$菁优网$
则 OP+PM≥OM．
∵⊙O半径为4，
∴PM≥OM-4≥OM'-4，
∵OA=OB．∠AOB=120°，
∴∠A=30°，
∴OM'=AM'•tan30°=12tan30°=4

，
∴PM≥OM'-4=4

-4，
∴线段PM的最小值为4

-4；
（2）如图②，分别在BC，AE上作BB'=AA'=r=30（m），
$菁优网$
连接A'B'，B'O、OP、OE、B′E．
∵OM⊥AB，BB'⊥AB，ON=BB'，
∴四边形BB'ON是平行四边形．
∴BN=B′O．
∵B'O+OP+PE≥B'O+OE≥B'E，
∴BN+PE≥B'E-r,
∴当点O在B'E上时，BN+PE取得最小值．
作⊙O'，使圆心O'在B'E上，半径r=30（m），
作O'M'⊥AB，垂足为M'，并与A'B'交于点H．
∴O'H∥A'E，
∴△B'O'H∽△B'EA'，
∴

＝

，
∵⊙O'在矩形AFDE区域内（含边界），
∴当⊙O'与FD相切时，B′H最短，即B′H=10000-6000+30=4030（m）．
此时，O′H也最短．
∵M'N'=O'H，
∴M'N'也最短．
∴O'H=

＝

=4017.91（m），
∴O'M'=O'H+30=4047.91（m），
∴此时环道⊙O的圆心O到AB的距离OM的长为4047.91m.

[点评]

本题考查了"等腰三角形的判定与性质,相似三角形的判定与性质,解直角三角形,切线的判定与性质,圆的综合题"，属于"难典题"，熟悉考点和题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

2770. （2020•益新中学•模拟）如图，AB是⊙O的直径，点C、E在⊙O上，∠B=2∠ACE，在BA的延长线上有一点P，使得∠P=∠BAC，弦CE交AB于点F，连接AE．
（1）求证：PE是⊙O的切线；
（2）若AF＝2，AE＝EF＝

，求OA的长．
$德优题库$

共享时间:2020-06-26 难度:3 相似度:1.35

解析

纠错

下载

组卷

198896. （2022•滨河中学•九上期中） $德优题库$ 如图，在Rt△ABC中，∠C=90°．已知AB=4，∠B=25°，求∠A，BC和AC的值（参考数据sin25°≈0.423，cos25°≈0.906，tan25°≈0.466，结果精确到0.1）

共享时间:2022-11-28 难度:1 相似度:1.2

解析

纠错

下载

组卷

189840. （2025•高新一中•九上期末）如图，在等腰直角△ABC中，∠ABC=90°，AB=6，P是线段AB上一个动点，连结CP，以CP为斜边构造等腰直角△CDP，M为CP的中点，连结AD，MB．
$德优题库$
【特值尝试】
（1）若AP=4，则BM= ，AD= ；
（2）设AP=x,△ADP的面积为y.
【周密思考】①求y关于x的函数表达式．
【问题解决】②记D关于直线AC的对称点为D′，当D′在△APC的外接圆上时，求此时△ADP的面积．

共享时间:2025-02-22 难度:1 相似度:1.2

解析

纠错

下载

组卷

185153. （2025•滨河中学•九下期中）如图，△ABC内接于⊙O，AB为⊙O的直径，延长BA至点D，使得∠ACD＝∠CBA．
（1）求证：CD是⊙O的切线；
（2）若BO＝5，

，求CD的长．

共享时间:2025-05-13 难度:5 相似度:1.2

解析

纠错

下载

组卷

185645. （2024•铁一中学•八下期中） $德优题库$ 已知：如图，在△ABC中，AB=AC，点E在CA的延长线上，EP⊥BC，垂足为P，EP交AB于点F．求证：△AEF是等腰三角形．

共享时间:2024-05-29 难度:1 相似度:1.2

解析

纠错

下载

组卷

189740. （2025•师大附中•八上期末）问题提出
学习了三角形的角平分线的定义之后，我们把三角形的三条内角平分线的交点叫做三角形的内心．
（1）如图①，已知△ABC的周长和面积都为30，点O是△ABC的内心，则点O到AB边的距离为．
问题探究
（2）如图②，在四边形ABCD中，AB=4，∠DAB=∠ABC=90°，以AB为边作等边△ABE，使得点E在边CD上且∠BEC=30°，点F是等边△ABE的内心，求点F到CD边的距离．
问题解决
（3）如图③所示的四边形ABCD为某公园的平面图，市政府计划在公园内部修建一个三角形广场即△ABE，点E到AB的距离为60m,在广场△ABE的边上装满彩灯，并在△ABE的内心F处修建喷泉供人们观赏，现需从喷泉F处到CD边上修建一条最短的地下水渠以便抽水．已知AB=2BC=80m,AD=100m,∠DAB=∠ABC=90°，据了解，彩灯每米30元，修建水渠每米60元，当彩灯费用最少时，装满彩灯和修建水渠的总花费是 .（结果保留根号）
$德优题库$

共享时间:2025-03-01 难度:1 相似度:1.2

解析

纠错

下载

组卷

189760. （2025•长安区•九上期末）如图，BE⊥AC于点E，AD⊥BC于点D．求证：

．

共享时间:2025-02-02 难度:1 相似度:1.2

解析

纠错

下载

组卷

189968. （2025•新城区•九上期末）【问题探究】
（1）如图1，△ABC内接于⊙O，AB＝BC，点D为劣弧

上任意一点（点D不与点A、C重合），连接AD、BD、CD，点D在运动的过程中始终有BD＝AD+DC，求∠ABC的度数；
【问题解决】
（2）如图2是一块半径为2米的圆形废旧铁皮，工人李叔叔计划从该铁皮上裁剪出一块四边形ABCD进行再利用，根据李叔叔的规划要求，点A，B，C，D均为⊙O上的点，AB＝BC，

BD＝AD+DC，请问该四边形ABCD的周长是否存在最大值？若存在，求出四边形ABCD周长的最大值；若不存在，请说明理由．

共享时间:2025-02-11 难度:1 相似度:1.2

解析

纠错

下载

组卷

180242. （2023•航天中学•八上二月）如图，在△ABC中，AB＝6，∠B＝30°，

，求边BC的长．

共享时间:2023-12-26 难度:1 相似度:1.2

解析

纠错

下载

组卷

190062. （2025•西咸新区•九上期末）如图，在Rt△ABC中，∠C＝90°，点D为AB的中点，DE⊥AB交AC于点E，连接BE，BE＝5，sin∠CBE＝

．
（1）求BC的长；
（2）求tanA的值．

共享时间:2025-02-08 难度:1 相似度:1.2

解析

纠错

下载

组卷

190107. （2025•未央区•九上期末） $德优题库$ 如图，在△ABC中，∠C=∠ADE，AB=3，AD=2，AC=8，求AE的长．

共享时间:2025-02-07 难度:1 相似度:1.2

解析

纠错

下载

组卷

190299. （2025•高新区•九上期末） $德优题库$ 问题提出：
（1）如图1，在△ABO中，OA=OB=4，∠AOB=120°，⊙O半径为1，点P是⊙O上的动点．则P到AB的最小值为；
问题探究：
（2）如图2，在正方形ABCD中，找出所有的点P，使得∠BPC=60°；
（3）问题解决：
如图3，有一个矩形水池ABCD，已知BC=30m,AB=20m.设计者想把水池分为四部分，分别是三角形AED，三角形CED，三角形BEC，三角形AEB．满足BF⊥AG，BF=2EF，点E在AG上，G为BC上的任意一点．若三角形CED区域养鱼，其他区域养虾．已知养鱼每平方米1000元，养虾每平方米800元．请问花费的最少费用是多少？

共享时间:2025-02-02 难度:1 相似度:1.2

解析

纠错

下载

组卷

190370. （2025•西工大附中•九上期末） $德优题库$ 如图，已知AB是⊙O的直径，直线BC与⊙O相切于点B，过点A作AD∥OC交⊙O于点D，连接CD．
（1）求证：CD是⊙O的切线．
（2）若AD=4，直径AB=12，求线段BC的长．

共享时间:2025-02-06 难度:1 相似度:1.2

解析

纠错

下载

组卷

190437. （2025•铁一中学•九上期末）在四边形ABCD中，对角线AC与BD相交于E，∠CAB=∠CBD，已知AB=4，AC=6，BC=5，BD=5.5，求DE的长．

共享时间:2025-02-25 难度:1 相似度:1.2

解析

纠错

下载

组卷

190442. （2025•铁一中学•九上期末） $德优题库$ 如图，⊙O的半径为4，B是⊙O外一点，连接OB，且OB=6，过点B作⊙O的切线BD，切点为D，延长BO交⊙O于点A，过点A作切线BD的垂线，垂足为C．
（1）求证：AD平分∠BAC；
（2）求AC的长．

共享时间:2025-02-25 难度:5 相似度:1.2

解析

纠错

下载

组卷

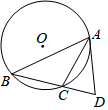
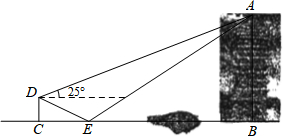
dyczsx2023

2023-07-20

初中数学 | | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2023年陕西省中考数学试卷（A卷）

更新:2023-07-20 04:17浏览量:839

普通登录

手机登录

微信扫码立即登录