服务热线
搜题▪组卷
 ,
,


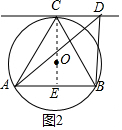
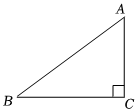 如图,在Rt△ABC中,∠C=90°.已知AB=4,∠B=25°,求∠A,BC和AC的值(参考数据sin25°≈0.423,cos25°≈0.906,tan25°≈0.466,结果精确到0.1)
如图,在Rt△ABC中,∠C=90°.已知AB=4,∠B=25°,求∠A,BC和AC的值(参考数据sin25°≈0.423,cos25°≈0.906,tan25°≈0.466,结果精确到0.1)
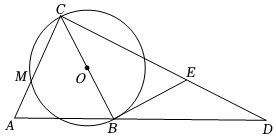 如图,△ABC中,AC=BC,以BC为直径作⊙O,交AC于点M,作CD⊥AC交AB延长线于点D,过点B作⊙O的切线BE,交CD于点E.
如图,△ABC中,AC=BC,以BC为直径作⊙O,交AC于点M,作CD⊥AC交AB延长线于点D,过点B作⊙O的切线BE,交CD于点E.





jdfz514
2018-06-06
初中数学 | | 解答题