服务热线
搜题▪组卷
的中点，点D在
上，且
＝2
，P是AB上的动点，试求PC+PD的最小值．
上选点P，在边OA上选点E，在边OB上选点F，用装饰灯带在花坛内的地面上围成一个△PEF，使晚上点亮时，花坛中的花卉依然赏心悦目．为了既节省材料，又美观大方，需使得灯带PE+EF+FP的长度最短，并且用长度最短的灯带围成的△PEF为等腰三角形．试求PE+EF+FP的值最小时的等腰△PEF的面积．（安装损耗忽略不计）
＝
＝4
，
．
＝
，
＝2
，
，DM＝OD•sin60°＝
，
，
＝
＝5
，
．
（m），
x+x＝20
，
﹣20）（m），
•PE•PF＝
（20
﹣20）2＝（600﹣400
）（m2）．
上任意一点（点D不与点A、C重合），连接AD、BD、CD，点D在运动的过程中始终有BD＝AD+DC，求∠ABC的度数；
BD＝AD+DC，请问该四边形ABCD的周长是否存在最大值？若存在，求出四边形ABCD周长的最大值；若不存在，请说明理由．
，∠AOB＝120°，点C是
上一点，则△ABC面积的最大值为 ；
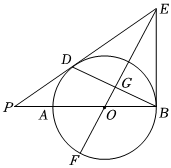如图，AB是⊙O的直径，BE与⊙O相切于点B，点D是⊙O上一点，连接ED并延长交BA的延长线于点P．连接BD、EO相交于点G，延长EO交⊙O于点F．若EO平分∠DEB，且EG⊥BD．
m，
，∠ABC＝45°，AD＝CD，∠ADC＝90°，弧ABC为⊙O上的一段优弧，点E为弧BC上的一点，过点E与点O铺设一条观赏小路EF，过点A铺设一条与之垂直的观赏小路AF，垂足为F，现计划在△FCD内种植牡丹花，已知牡丹花每平米的成本费为500元，则种植牡丹花所需费用至少为多少元？
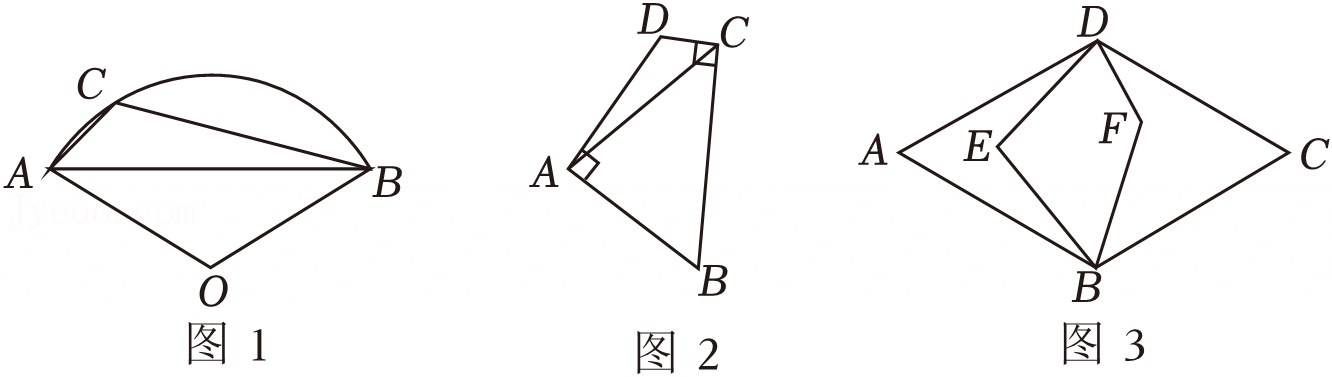
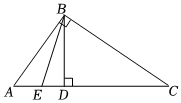如图，在△ABC中，∠ABC=90°，过点B作BD⊥AC于点D，BE平分∠ABD交AC于点E．
的中点，桥下水面的宽度AB=24m,点P到水面AB的距离PH=8m.点P1，P2均在上，
=
，且P1P2=10m,在点P1，P2处各装有一个照明灯，图中△P1CD和△P2EF分别是这两个灯的光照范围．两灯可以分别绕点P1，P2左右转动，且光束始终照在水面AB上．即∠CP1D，∠EP2F可分别绕点P1，P2按顺（逆）时针方向旋转（照明灯的大小忽略不计），线段CD，EF在AB上，此时，线段ED是这两灯照在水面AB上的重叠部分的水面宽度．已知∠CP1D=∠EP2F=90°，在这两个灯的照射下，当整个水面AB都被灯光照到时，求这两个灯照在水面AB上的重叠部分的水面宽度．（可利用备用图解答）
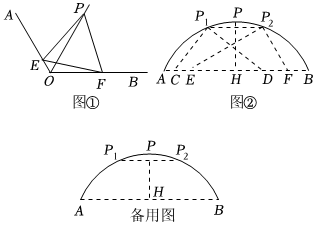
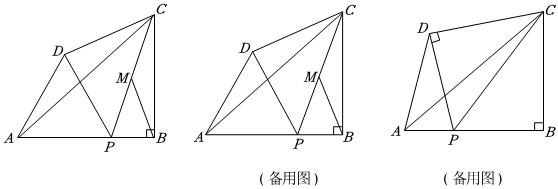
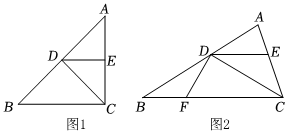已知在△ABC中，∠ACB的平分线CD交AB于点D，DE∥BC．亦世凡华
2018-07-03
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
已知：如图，在△ABC中，AB=AC，点E在CA的延长线上，EP⊥BC，垂足为P，EP交AB于点F．求证：△AEF是等腰三角形．
