服务热线
搜题▪组卷
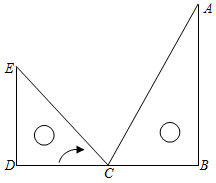
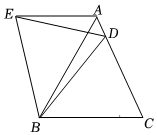 在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC.其中正确的序号是 .(请填写序号)
在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC.其中正确的序号是 .(请填写序号)
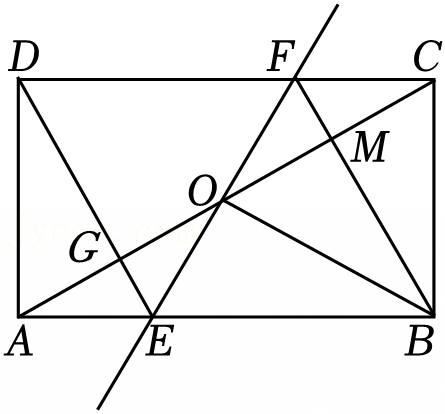
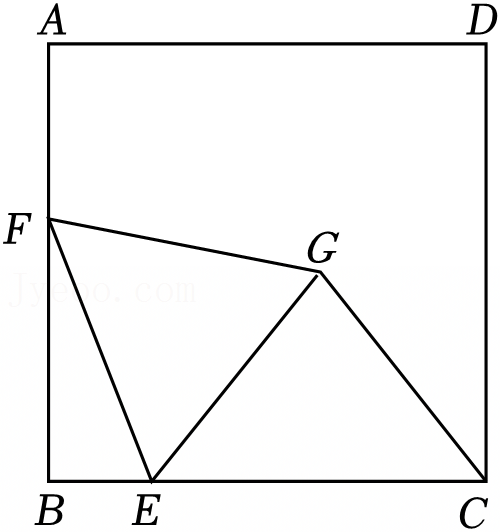
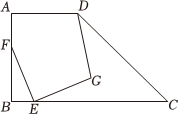
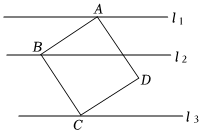 如图,直线l1∥l2∥l3,正方形ABCD的三个顶点A、B、C分别在l1、l2、l3上,l1与l2之的距离是2,l2与l3之间的距离是4,则正方形ABCD的面积为 .
如图,直线l1∥l2∥l3,正方形ABCD的三个顶点A、B、C分别在l1、l2、l3上,l1与l2之的距离是2,l2与l3之间的距离是4,则正方形ABCD的面积为 .

sa@dyw.com
2022-05-18
初中数学 | 八年级下 | 填空题