服务热线
搜题▪组卷
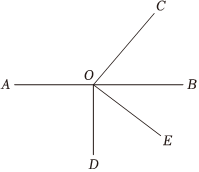点O在直线AB上，∠COE=90°，∠AOD=90°．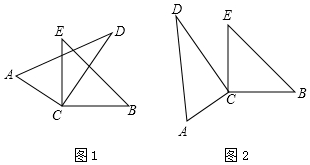
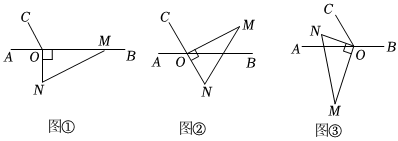
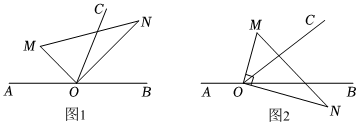
如图，将一副三角板中两个直角顶点重合于点O，按如图方式叠放在一起．
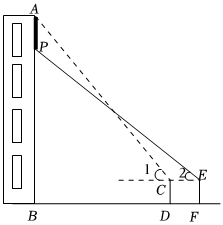校训是一个学校的灵魂，体现了一所学校的办学传统，代表着校园文化和教育理念，是人文精神的高度凝练，是学校历史和文化的积淀．小颖在数学综合实践活动中，利用所学的数学知识测量学校教学楼上校训牌的高度AP，如图，她先在教学楼前的D处测得校训牌上端A处的仰角为∠1，然后她后退2m到达F处，又测得该校训牌下端P处的仰角为∠2，发现∠1与∠2恰好互余，已知教学楼的高AB=12m,BD=8.5m,小颖的眼睛离地面的距离CD=EF=1.5m,且A，P，B三点共线，AB⊥BF，CD⊥BF，EF⊥BF，校训牌的顶端与教学楼顶端平齐，请你根据以上信息帮助她求出校训牌的高度AP．
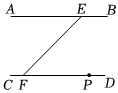如图，已知AB∥CD，点E在AB上，点F、P在CD上，连接EF，请用尺规作图法在AE上求作一点H，连接PH交EF于点O，使得∠OHE与∠OFP互余．（保留作图痕迹，不写作法）
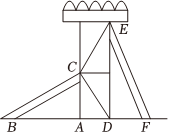如图，已知两个滑梯BC和EF的倾斜角∠ABC和∠DFE互为余角（即∠ABC+∠DFE=90°），且左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，且AC⊥BF，ED⊥BF．小明说：“只要量出左侧滑梯水平方向的长度AB就可以知道右侧滑梯的高度DE了”，他的说法正确吗？请你说明理由．
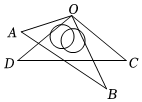
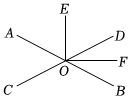如图，直线AB，CD相交于点O，分别作∠AOD，∠BOD的平分线OE，OF．
dyczsxyn
2024-11-13
初中数学 | 七年级上 | 解答题
纠错
收藏
下载
相似
组卷
已知O为直线AB上一点，∠COE=90°，OF平分∠AOE．若∠COF=35°，求∠AOC、∠BOE的度数．
解析
如图，直线a,b,c被直线l所截，其中∠1+∠2=180°，∠2+∠4=180°．求证：a∥c.
如图，∠1+∠2=180°，∠DEF=∠A，求证：AC∥DE．