服务热线
搜题▪组卷
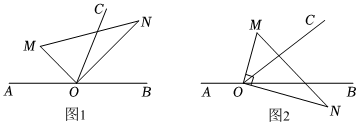
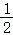
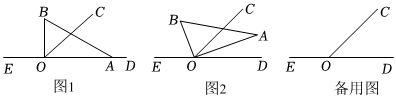
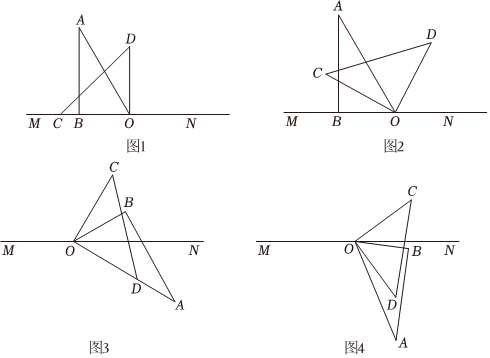
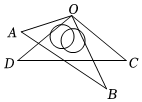 如图,将一副三角板中两个直角顶点重合于点O,按如图方式叠放在一起.
如图,将一副三角板中两个直角顶点重合于点O,按如图方式叠放在一起.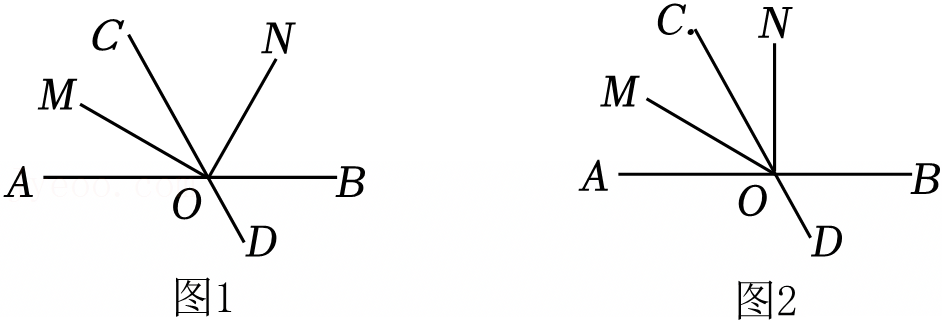
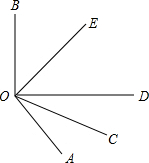 如图,OC是∠AOD的平分线,OE是∠BOD的平分线,∠AOB=130°.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线,∠AOB=130°.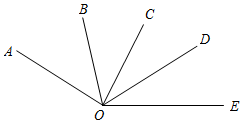

ydy@dyw.com
2023-02-18
初中数学 | 七年级上 | 解答题