服务热线
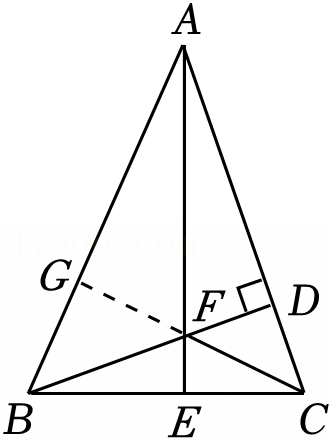
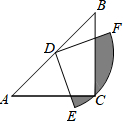
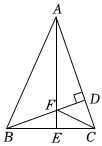如图，在△ABC中，BD是AC边上的高，∠AEB=90°，BC=AF，则下列结论正确的有：（ ）
，
BF•AD＝
BF•BD，S△CBF＝
BF•DC＝
BF•DF，
＝
＝
，即S△ABF：S△CBF＝BD：DF，
AD•EF；④CE2+BE2＝2AE2，其中正确的是（ ）
如图，已知△ABC和△ADE都是等腰三角形，∠BAC=∠DAE=90°，BD，CE交于点F，连接AF，下列结论：①BD=CE；②BF⊥CF；③AF平分∠CAD；④∠AFE=45°．其中正确结论的个数有（ ）
如图，△BDC为等腰直角三角形，延长BD至A，连接AC，作∠ABC的角平分线BE交DC于F，且BE⊥AC于E．若AE=12，△ABC的面积为360，则EF的长度为（ ）
）
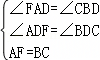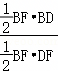A.面积为π-2
C.面积为
π﹣1
B.面积为2π-4
D.面积随扇形位置的变化而变化
；（5）AD2+BE2＝2DM2；（6）四边形CDME的面积随点D的运动而变化．其中正确的结论有（ ）
如图，把两个45°角的直角三角板放在一起，点B在CE上，A、C、D三点在一条直线上，连接AE，DB延长线交AE于点F．若AE=8，DF=11.2，则△ABE的面积为（ ）
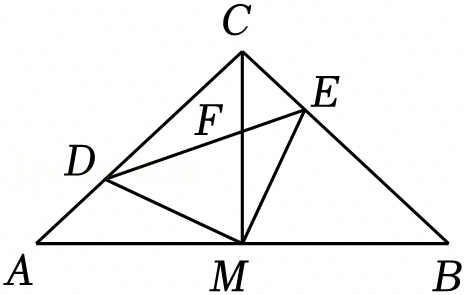
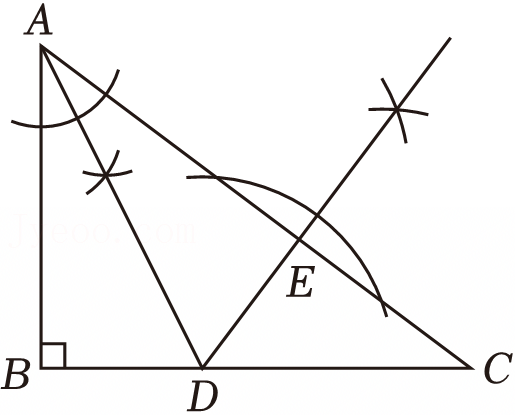
A.只有甲对
C.只有乙对
B.．只有丙对
D.三人说的都对
dyczsxyn
2024-07-21
初中数学 | 七年级下 | 选择题
纠错
收藏
下载
相似
组卷
解析
如图，在四边形ABCD中，AB∥CD，∠D=90°，∠ABC与∠BCD的平分线交AD于点E．若BC=16，AD=12，则四边形ABCD的周长为（ ）
如图所示，点A、B、C、D均在正方形网格格点上，则∠B+∠D=（ ）
如图，在△ABC中，∠BAC=45°，AD⊥BC于点D，CE⊥AB于点E，AD和CE交于点F，若AB=7，BE=3，则DF的长为（ ）
