服务热线
搜题▪组卷
是某新区的三条规划路，其中AB=6km，AC=3km，∠BAC=60°，
所对的圆心角为60°，新区管委会想在
路边建物资总站点P，在AB，AC路边分别建物资分站点E、F，也就是，分别在
、线段AB和AC上选取点P、E、F．由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP．为了快捷、环保和节约成本．要使得线段PE、EF、FP之和最短，试求PE+EF+FP的最小值．（各物资站点与所在道路之间的距离、路宽均忽略不计）
AB=12，
r，
r，
，
，
，
，
﹣3
，
r=3
﹣9
﹣9）km．
于点E，又测得DE=8m．
＝2
，连接OE、AF，过点B作⊙O的切线，分别与OE、AF的延长线交于点C、D．
，且OC＝4，求PA的长．
cm，连接AC、BD、BC，把△ABC沿BC折叠得△A1BC．
，求⊙O的半径．
+1，小明根据学习反比例函数y＝
的经验，对函数y＝
+1的图象和性质进行了探究．
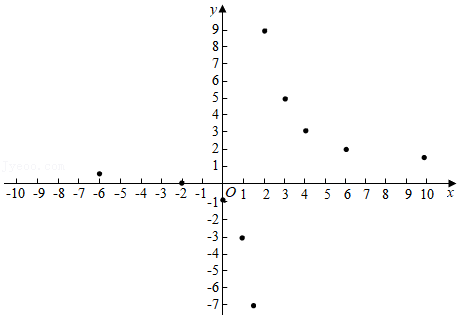
+1的自变量x的取值范围是______；| x | … | ﹣6 | ﹣2 | 1 | 0 |  |
 |
3 | 4 | 6 | 10 | … |
| y | … |  |
0 | ﹣3 | ﹣1 | ﹣7 | 9 | 5 | 3 | 2 |  |
… |
的图象和性质，结合画出的函数y＝
+1图象，回答下列问题：
的图象平移得到的，其平移方式为__________；
+1≥﹣1时x的取值范围____________．
的中点，点D在
上，且
＝2
，P是AB上的动点，试求PC+PD的最小值．
上选点P，在边OA上选点E，在边OB上选点F，用装饰灯带在花坛内的地面上围成一个△PEF，使晚上点亮时，花坛中的花卉依然赏心悦目．为了既节省材料，又美观大方，需使得灯带PE+EF+FP的长度最短，并且用长度最短的灯带围成的△PEF为等腰三角形．试求PE+EF+FP的值最小时的等腰△PEF的面积．（安装损耗忽略不计）
艺黎
2018-07-02
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
