服务热线
搜题▪组卷
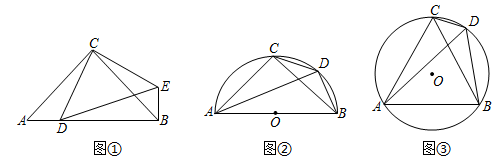
 如图,在等边△ABC中,AE与CD交于点F.给出下列两个条件:①EC=DB,②∠ADC=∠BEA.
如图,在等边△ABC中,AE与CD交于点F.给出下列两个条件:①EC=DB,②∠ADC=∠BEA.

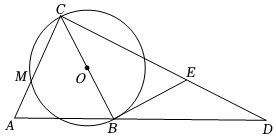 如图,△ABC中,AC=BC,以BC为直径作⊙O,交AC于点M,作CD⊥AC交AB延长线于点D,过点B作⊙O的切线BE,交CD于点E.
如图,△ABC中,AC=BC,以BC为直径作⊙O,交AC于点M,作CD⊥AC交AB延长线于点D,过点B作⊙O的切线BE,交CD于点E.时光温润
2014-09-18
初中数学 | | 解答题