服务热线
搜题▪组卷
试卷总分:120分 命题人:csyn@dyw.com 考试时长:120分钟
A.
|
B.
|
C.
|
D.
|
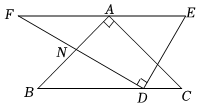将一副直角三角板如图放置，已知∠E=60°，∠C=45°，EF∥BC，则∠BND的大小为（ ）
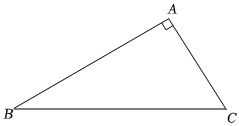已知：Rt△ABC中，∠BAC=90°，∠B=30°，请你用尺规在Rt△ABC的边AB上求作一点M，使得点M到BC的距离等于AM．（保留作图痕迹，不写作法）
无人机在实际生活中的应用广泛，如图所示，某人利用无人机测大楼的高度BC，无人机在空中点A处，测得点A与地面距离80米，测得C点的俯角为14°，控制无人机水平移动至点D，测得AD=21米，楼顶C点的俯角为31°，（点A、B、C、D在同一平面内），求大楼的高度BC．（tan14°=0.25，tan31°=0.6）
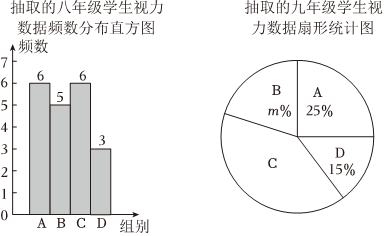
| 平均数 | 中位数 | 众数 | |
| 八年级 | 4.82 | a | 4.9 |
| 九年级 | 4.82 | 4.8 | 4.7 |
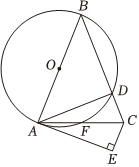如图，在△ABC中，AB=BC，以AB为直径的⊙O交BC于点D，交AC于点F，在AC下方作∠CAE=∠CAD，过点C作CE⊥AE，垂足为点E．| 素材1 | 一圆形喷泉池的中央安装了一个喷水装置OA，通过调节喷水装置OA的高度，从而实现喷出水柱竖直方向的升降，但不改变水柱的形状．为了美观在半径为2.1米的喷泉池四周种植了一圈宽度均相等的花卉（图1中的阴影部分）． |  |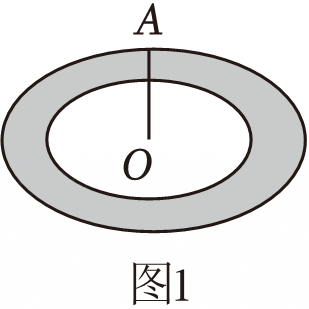
| 素材2 | 从喷泉口A喷出的水柱成抛物线形，如图2是该喷泉喷水时的一个截面示意图，已知喷水口A离地面高度为0.72米，喷出的水柱在离喷水口水平距离为0.3米处离地面最高，高度为0.75米． |  |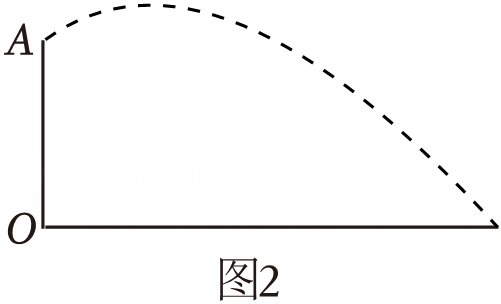
| 问题解决 | ||
| 任务1 | 建立模型 | 以点O为原点，OA所在直线为y轴建立平面直角坐标系，根据素材2求抛物线的函数表达式． |
| 任务2 | 利用模型 | 为了提高对水资源的利用率，在欣赏喷泉之余也能喷灌四周的花卉，确定喷水口A升高的最小值． |
| 任务3 | 分析计算 | 喷泉口A升高的最大值为 米，为能充分喷灌四周花卉，请对花卉的种植宽度提出合理的建议． |
BD长为半径的圆；△BCD的外接圆也是以BD的中点为圆心，
BD长为半径的圆．这样A、B、C、D四点在同一个圆上，进而可以利用圆周角的性质求出∠BDC 的度数，请运用小底的思路解决这个问题．
csyn@dyw.com
2024-03-21
初中数学 | 中考 | 难度:1.96
| 下载试卷 | 收藏 |
| 平行组卷 | 细目重组 |
| 试卷分析 | 加入白板 |
| 加卷篮 | 更多功能 |
平行组卷卷生成中,请等待
解析
纠错
收藏
下载
相似
组卷
大自然巧夺天工，一片树叶也蕴含着“黄金分割”．如图，P为AB的黄金分割点（AP＞PB），如果AB的长度为8cm,那么PB的长度是 cm.
如图，在矩形ABCD中，AB=8，BC=12，点E是BC的中点，连接AE，将△ABE沿AE折叠，点B落在点F处，连接FC，则sin∠ECF= ．
如图，AC=BD，CE=DE，AD与BC相交于点E，∠EAB=∠EBA．求证：△ACB≌△BDA．
