首页 > 试卷详情

德优网2021陕西省西安市未央区西安中学高中数学段考月考高三上

2021-2022学年陕西省西安中学高三（上）第一次质检数学试卷（理科）

试卷总分:150分命题人:dygzsxyn 考试时长:120分钟

一、选择题(12小题共60分)

1. （本题5分）已知集合A＝{x|lnx＜0}，

，则A∩∁_RB＝（　　）

C.（1，+∞）

解析

纠错

下载

相似

组卷

2. （本题5分）已知命题p：“∀x＞0，都有3^x＞1”的否定是“∃x≤0，使3^x≤1”；
命题q：“a，b∈R，若a²+b²＝0，则a＝b＝0”的否命题是“a，b∈R，若a²+b²≠0，则a≠0或b≠0”；
下列命题为真命题的是（　　）

A.p∧q

B.p∨（￢q）

C.（￢p）∧q

D.（￢p）∧（￢q）

解析

纠错

下载

相似

组卷

3. （本题5分）已知函数f（x）＝

，则f（log₂7）的值为（　　）

A.	B.
C.	D.

解析

纠错

下载

相似

组卷

4. （本题5分）设a＝

，b＝

，c＝

，则a，b，c的大小关系（　　）

A.a＞b＞c

B.a＞c＞b

C.b＞a＞c

D.b＞c＞a

解析

纠错

下载

相似

组卷

5. （本题5分）公元前6世纪，古希腊毕达哥拉斯学派在研究正五边形和正十边形的作图时，发现了黄金分割数

，其近似值为0.618，这是一个伟大的发现，这一数值也表示为a＝2sin18°，若a²+b＝4，则

＝（　　）

B.2

D.4

解析

纠错

下载

相似

组卷

6. （本题5分）函数f（x）＝（x²﹣2x）e^x的图象大致是（　　）

A. $德优题库$	B. $德优题库$
C. $德优题库$	D. $德优题库$

解析

纠错

下载

相似

组卷

7. （本题5分）下列函数中，图像关于原点对称且在区间（﹣1，1）上单调递增的是（　　）

A.	B.
C.	D.f（x）＝2^x﹣2^﹣x

解析

纠错

下载

相似

组卷

8. （本题5分）已知sinα＝

，sin（α﹣β）＝﹣

，α，β均为锐角，则β＝（　　）

解析

纠错

下载

相似

组卷

9. （本题5分）定义在R上的可导函数f（x），当x∈（1，+∞）时，（x﹣1）f′（x）﹣f（x）＞0恒成立，a＝f（2），b＝

f（3），c＝（

+1）f（

），则a、b、c的大小关系为（　　）

A.c＜a＜b

B.b＜c＜a

C.a＜c＜b

D.c＜b＜a

解析

纠错

下载

相似

组卷

10. （本题5分）中国的5G技术领先世界，5G技术的数学原理之一便是著名的香农公式：

．它表示：在受噪音干扰的信道中，最大信息传递速度C取决于信道带宽W，信道内信号的平均功率S，信道内部的高斯噪声功率N的大小，其中

叫做信噪比．当信噪比比较大时，公式中真数里面的1可以忽略不计．按照香农公式，若带宽W增大到原来的1.1倍，信噪比

从1000提升到16000，则C大约增加了（　　）（附：lg2≈0.3）

A.21%

B.32%

C.43%

D.54%

解析

纠错

下载

相似

组卷

11. （本题5分）已知f（x）是定义在R上的函数，且对任意x∈R都有f（x+2）＝f（2﹣x）+4f（2），若函数y＝f（x+1）的图象关于点（﹣1，0）对称，且f（1）＝3，则f（2021）＝（　　）

A.6

B.3

C. 0

D.-3

解析

纠错

下载

相似

组卷

12. （本题5分）已知函数f（x）＝

，函数g（x）＝f（x）+m有3个不同的零点x₁，x₂，x₃，且x₁＜x₂＜x₃，则

的取值范围是（　　）

A.[，）	B.[ln2，ln6）
C.[﹣1，）	D.[0，）

解析

纠错

下载

相似

组卷

二、填空题(4小题共20分)

13. （本题5分）已知函数f（x）=x-xcosx,则f（x）在区间[0，π]上的最大值是．

解析

纠错

下载

相似

组卷

14. （本题5分）折扇是一种用竹木做扇骨，韧纸或绫绢做扇面的能折叠的扇子．如图，某折扇的扇骨长度OA＝15cm，扇面长度AB＝10cm，已知折扇展开所对圆心角的弧度为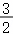

，则扇面的面积为　　．

解析

纠错

下载

相似

组卷

15. （本题5分）已知直线y=x+1与曲线y=lnx+a相切，则a的值为．

解析

纠错

下载

相似

组卷

16. （本题5分）已知函数f（x）=e^x+ax-3（a∈R），若对于任意的x₁，x₂∈[1，+∞）且x₁＜x₂，都有x₂f（x₁）-x₁f（x₂）＜a（x₁-x₂）成立，则a的取值范围是．

解析

纠错

下载

相似

组卷

三、解答题(6小题共70分)

17. （本题10分）已知函数f（x）＝cos（2x﹣

）+2sin（x﹣

）sin（x+

）．
（Ⅰ）求函数f（x）的最小正周期和图象的对称轴方程；
（Ⅱ）求函数f（x）在区间

上的值域．

解析

纠错

下载

相似

组卷

18. （本题12分）已知函数f（x）=|mx-1|+|2x-1|．
（1）当m=1时，求不等式f（x）≤2的解集；
（2）若f（x）≤2x+1在x∈[1，2]上恒成立，求m的取值范围．

解析

纠错

下载

相似

组卷

19. （本题12分）在直角坐标系xOy中，以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C的极坐标方程为ρ＝sinθ+cosθ，点P在曲线C上运动．
（1）若点Q在射线OP上，且|OP|•|OQ|＝4，求点Q的轨迹的直角坐标方程；
（2）设

，求△MOP面积的最大值及此时点P的坐标．

解析

纠错

下载

相似

组卷

20. （本题12分）已知f（e^x）＝x﹣2e^x﹣3．
（1）求函数f（x）的解析式；
（2）求函数f（x）的值域；
（3）若函数

在定义域上是增函数，求实数k的取值范围．

解析

纠错

下载

相似

组卷

21. （本题12分）某客户准备在家中安装一套净水系统，该系统为二级过滤，使用寿命为十年．如图1所示，两个二级过滤器采用并联安装，再与一级过滤器串联安装
$德优题库$
其中每一级过滤都由核心部件滤芯来实现．在使用过程中，一级滤芯和二级滤芯都需要不定期更换（每个滤芯是否需要更换相互独立）．客户在安装净水系统的同时购买滤芯和在使用过程中单独购买滤芯的情况如下表：

	一级滤芯	二级滤芯
安装净水系统的同时购买	160元/个	80元/个
使用过程中单独购买	200元/个	100元/个

现需决策安装净水系统的同时购买滤芯的数量，为此参考了根据100套该净水系统在十年使用期内更换的滤芯的相关数据制成的图表，其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表，图2是根据200个二级过滤器更换的滤芯个数制成的条形图．
表1：一级滤芯更换频数分布表

一级滤芯更换的个数	8	9
频数	60	40

以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率，以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率．
（Ⅰ）记Y表示该客户的净水系统在使用期内需要更换的一级滤芯总数，求Y的分布列及数学期望；
（Ⅱ）求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为21的概率；
（Ⅲ）记m,n分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数．若m+n=18且m∈{8，9}，以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据，试确定m,n的值．

解析

纠错

下载

相似

组卷

22. （本题12分）设函数f（x）＝xlnx﹣

+a﹣x（a∈R）．
（1）若函数f（x）有两个不同的极值点，求实数a的取值范围；
（2）若a＝2，k∈N，g（x）＝2﹣2x﹣x²，且当x＞2时不等式k（x﹣2）+g（x）＜f（x）恒成立，试求k的最大值．

解析

纠错

下载

相似

组卷

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

dygzsxyn

2021-10-22

高中数学 | 段考 | 难度:1.27

下载量
浏览量
收益额

下载试卷	收藏
平行组卷	细目重组
试卷分析	加入白板
加卷篮	更多功能

同类试卷 更多>>

2023-2024学年陕西省西安市长安一中高三（上）第二次质检数学试卷（理科）

更新:2023-12-15 12:58浏览量:35

2024-2025学年陕西省西安市铁一中学高一（上）第一次月考数学试卷

更新:2024-10-26 12:41浏览量:237

2024-2025学年陕西师大附中高一（上）月考数学试卷（12月份）

更新:2024-12-16 04:45浏览量:56

2024-2025学年陕西师大附中高二（上）月考数学试卷（12月份）

更新:2024-12-29 01:34浏览量:77

2024-2025学年陕西师大附中高二（上）月考数学试卷（10月份）

更新:2024-10-30 09:24浏览量:45

2024-2025学年陕西省西安市高新一中高二（上）第二次月考数学试卷

更新:2024-12-27 01:45浏览量:98

2024-2025学年陕西省西安中学高三（上）第二次质检数学试卷

更新:2024-12-28 03:32浏览量:81

2024-2025学年陕西省西安中学高二（上）月考数学试卷（12月份）

更新:2024-12-23 07:46浏览量:45

2024-2025学年陕西省西安西北工大附中高一（上）第二次月考数学试卷（12月份）

更新:2024-12-29 01:12浏览量:92

2024-2025学年陕西省西安市长安一中高三（上）第四次月考数学试卷

更新:2024-02-12 04:00浏览量:35

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

微信扫码立即登录

AI助手

2021-2022学年陕西省西安中学高三（上）第一次质检数学试卷（理科）

登录

注册

微信扫码立即登录

AI助手

2021-2022学年陕西省西安中学高三（上）第一次质检数学试卷（理科）