已知函数当时证明讨论函数零点的个数

首页 > 试题列表 > 单题解析

237273. （2021•西安中学•高二下期中）已知函数f（x）＝e^x﹣ax﹣1（a∈R）．
（1）当a＝1时，证明f（x）≥0；
（2）讨论函数f（x）零点的个数．

共享时间:2021-05-12 难度:2

纠错

下载

相似

组卷白板

[考点]

函数的零点与方程根的关系，利用导数研究函数的最值，

[答案]

（1）当a∈（﹣∞，0]∪{1}时，有1个零点；当a∈（0，1）∪（1，+∞）时，有2个零点．

（2）答案见解析．

[解析]

（1）证明：当a＝1时，f（x）＝e^x﹣x﹣1，则f'（x）＝e^x﹣1，
当x＜0时，f'（x）＜0，f（x）单调递减，
当x＞0时，f'（x）＞0，f（x）单调递增，
即当x＝0时，f（x）_min＝f（0）＝0，所以f（x）≥0．
（2）解：因为函数f（x）＝e^x﹣ax﹣1（a∈R），则f'（x）＝e^x﹣a，
当a≤0时，f'（x）＞0，则f（x）单调递增，且f（0）＝e⁰﹣1＝0，
所以f（x）在R上只有一个零点；
当a＞0时，令f'（x）＝0，可得x＝lna，
由f'（x）＜0，得x＜lna，由f'（x）＞0，得x＞lna，
且f（lna）＝e^lna﹣alna﹣1＝a﹣alna﹣1，
令g（a）＝a﹣alna﹣1，则g'（a）＝﹣lna，
由﹣lna＝0，可得a＝1，则0＜a＜1时，g'（a）＞0，a＞1时，g'（a）＜0，
所以（0，1）上g（a）递增，（1，+∞）上g（a）递减，故g（a）≤g（1）＝0，
所以f（lna）≤0，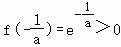

，x趋向正无穷则f（x）趋于正无穷，
此时，当a∈（0，1）∪（1，+∞）时有两个零点，当a＝1时有一个零点，
综上，当a∈（﹣∞，0]∪{1}时，有1个零点；当a∈（0，1）∪（1，+∞）时，有2个零点．

[点评]

本题考查了"函数的零点与方程根的关系，利用导数研究函数的最值，"，属于"易错题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

168253. （2021•西安中学•五模）已知函数f（x）＝e^x﹣1﹣ax（a∈R）．
（1）试讨论函数f（x）的零点个数；
（2）若函数g（x）＝ln（e^x﹣1）﹣lnx，且f[g（x）]＜f（x）在x∈（0，+∞）上恒成立，求实数a的取值范围．

共享时间:2021-05-01 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

167855. （2024•西工大附中•模拟）已知函数f（x）＝ax﹣lnx﹣a，且f（x）≥0．
（1）求a；
（2）设g（x）＝x•f（x），证明：g（x）存在唯一的极大值点x₀，且g（x₀）＜

．

共享时间:2024-03-05 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

168082. （2023•西工大附中•十三模）已知函数f（x）＝e^x（1+alnx），其中a＞0，设f′（x）为f（x）导函数．
（Ⅰ）设g（x）＝e^﹣xf′（x），若g（x）≥2恒成立，求a的范围；
（Ⅱ）设函数f（x）的零点为x₀，函数f′（x）的极小值点为x₁，当a＞2时，求证：x₀＞x₁．

共享时间:2023-07-27 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

166836. （2024•西安八十五中•一模）已知函数f（x）＝a^2x+a^﹣2x+m（a^x﹣a^﹣x）（a＞0且a≠1）．
（1）若m＝2，求函数f（x）的最小值；
（2）若f（x）≥﹣1恒成立，求实数m的取值范围．

共享时间:2024-03-12 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

168851. （2021•西工大附中•十二模）．已知函数f（x）＝lnx，g（x）＝x²．
（1）若不等式f（x）≤ax﹣1对x∈（0，+∞）恒成立，求实数a的范围；
（2）若正项数列{a_n}满足a₁＝

，a_n₊₁＝

，数列{a_n}的前n项和为S_n，求证：

+1．

共享时间:2021-07-22 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

168105. （2023•西工大附中•十三模）已知函数f（x）＝e^x（1+alnx），其中a＞0，设f′（x）为f（x）导函数．
（Ⅰ）设g（x）＝e^﹣xf′（x），若g（x）≥2恒成立，求a的范围；
（Ⅱ）设函数f（x）的零点为x₀，函数f′（x）的极小值点为x₁，当a＞2时，求证：x₀＞x₁．

共享时间:2023-07-20 难度:1 相似度:1.5

解析

纠错

下载

组卷白板