服务热线
搜题▪组卷
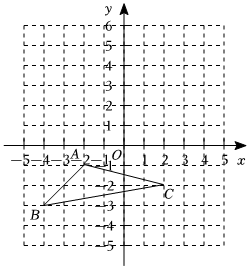如图，在平面直角坐标系中，已知A（-2，-1），B（-4，-3），C（2，-2）．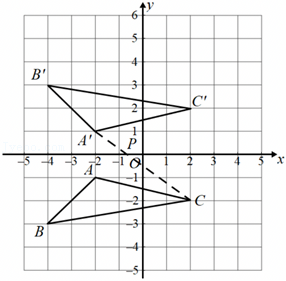
；
，
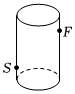如图，圆柱形玻璃杯高18cm,底面周长为60cm,在外侧距下底处1cm有一只蜘蛛，与蜘蛛相对的圆柱形容器的上端距开口处1cm的外侧点处有一只苍蝇，试求蜘蛛捕到苍蝇的最短路线长是多少．
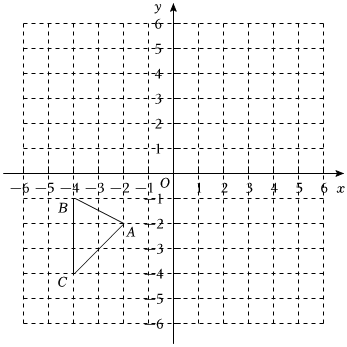如图所示，在平面直角坐标系中，△ABC的三个顶点分别是A（-2，-2）、B（-4，-1）、C（-4，-4）．
m，计划在空地的一角打造以“非遗文化创意手工展”为主题的长廊BC，长度为60
m，若空地边界AD上的点P为出入口，点M，N分别为两个休息点，且AM＝150m，N为BC的中点，出入口P到休息点M，N各有一条通道MP，NP．请问：是否存在满足条件的点P，使得通道MP，NP的长度之和最短？若存在，求此时MP，NP的长度之和；若不存在，请说明理由．（图中各点均在同一平面内，街道AE与通道MP，NP的宽、休息点及出入口的大小均忽略不计，结果保留根号）
）三点．
的中点，点D在
上，且
＝2
，P是AB上的动点，试求PC+PD的最小值．
上选点P，在边OA上选点E，在边OB上选点F，用装饰灯带在花坛内的地面上围成一个△PEF，使晚上点亮时，花坛中的花卉依然赏心悦目．为了既节省材料，又美观大方，需使得灯带PE+EF+FP的长度最短，并且用长度最短的灯带围成的△PEF为等腰三角形．试求PE+EF+FP的值最小时的等腰△PEF的面积．（安装损耗忽略不计）
，求∠MAN的度数；
，求裁剪长度（OM+ON）的最小值．
米，∠EHG=45°，经研究，只有当点E、F、G分别在边AD、AB、BC上，且AF＜BF，并满足点H在矩形ABCD内部或边上时，才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形EFGH部件？若能，求出裁得的四边形EFGH部件的面积；若不能，请说明理由．
，且点O、E、D′在同一条直线上？若存在，请求出m的值；若不存在，请说明理由．
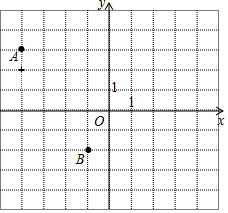如图，在平面直角坐标系中，已知A（-4，3），B（-1，-2）．
bs@dyw.com
2023-11-19
初中数学 | 八年级上 | 解答题
纠错
收藏
下载
相似
组卷
解析
