三、解答题(12小题共81分)
14.
(本题5分)
计算: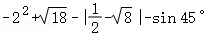 .
.
15.
(本题5分)
解方程:x2-5x-4=0.
16.
(本题6分)
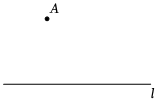 如图,已知直线l和l外一点A,请用尺规作图法,求作一个正方形ABCD,使得顶点B和顶点D都在直线l上(保留作图痕迹,不写作法)
如图,已知直线l和l外一点A,请用尺规作图法,求作一个正方形ABCD,使得顶点B和顶点D都在直线l上(保留作图痕迹,不写作法)
17.
(本题6分)
先化简,再求值: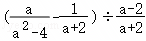 ,其中a=tan45°.
,其中a=tan45°.
18.
(本题6分)
在四边形ABCD中,对角线AC与BD相交于E,∠CAB=∠CBD,已知AB=4,AC=6,BC=5,BD=5.5,求DE的长.
19.
(本题6分)
某空调生产厂的装配车间计划在一段时期内组装5000台空调.计划在x天内完成全部组装,设平均每天组装的空调数量为y(台/天).
(1)直接写出y与x之间的函数关系式;
(2)原计划用50天完成这一任务,但由于气温提前升高,厂家决定提前10天完成这批空调的组装,那么装配车间平均每天要组装多少台空调?
20.
(本题6分)
一年一度的校园新年音乐会即将开始,九年级三班的小颍与小亮都想去观看,但学校给每个班只发一张门票,于是两人想通过摸卡片的方式来决定谁去观看.规则如下:现有两组卡片,第一组卡片上写有A,B,C,第二组卡片上写有A,B,B,C,这两组卡片上除字母外其余均相同.将卡片正面朝下洗匀,随机抽取一张,记下字母后放回,称为摸卡片一次.
(1)若小颖从第二组中的机抽取一张卡片,则抽取到B的概率为 ;
(2)小亮从第一组中摸卡片一次,小颖从第二组中摸卡片一次,若两人摸出的卡片上所写字母相同,则小颖去观看,如果两人摸出的卡片上所写字母不相同,则小亮去观看.请用列表或画树状图的方法,判断这个规则对两个人公平吗?
21.
(本题7分)
某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少小分支?
22.
(本题7分)
如图1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示意图如图2,此时测得点A到BC所在直线的距离AC=3m,∠CAB=60°,停止位置示意图如图3,此时测得∠CDB=37°(点C,A,D在同一直线上,且直线CD与地面平行),图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子总长不变.
(1)求AB的长;
(2)求物体上升的高度CE(结果精确到0.1m).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,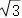 ≈1.73)
≈1.73)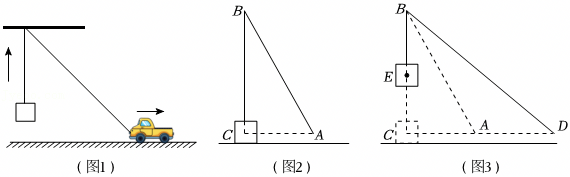
23.
(本题8分)
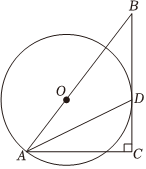 如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
(1)求证:AD平分∠BAC;
(2)求AC的长.
24.
(本题9分)
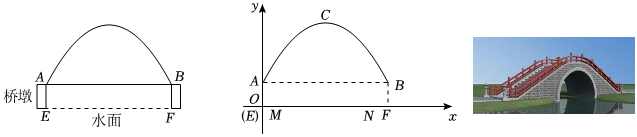
某公园内人工湖上有一座拱桥(横截面如图所示),跨度AB为4米,桥墩AE与BF的高为0.88米,拱桥最高点到水面距离为2.88米.
(1)建立如图所示的直角坐标系,求此抛物线的函数表达式;
(2)公园欲开设游船项目,其中豪华游船长为3.3米,宽为2.7米,露出水面高度为1.88米.为安全起见,游船经过拱桥时,游船顶部和拱桥至少有0.2米的安全距离.公园要在水面上的M,N两处设置警戒线.并且ME=NF,要求游船能从M,N两点之间安全通过,则M处距桥墩的距离ME至少为多少米?(结果保留根号)
25.
(本题10分)
问题提出
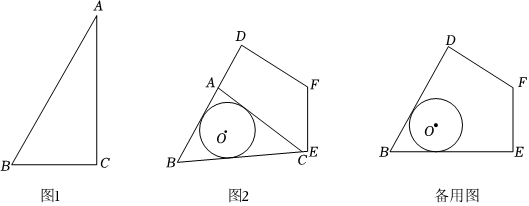
(1)如图1,在直角△ABC中,∠A=30°,⊙I是△ABC的内切圆,若⊙I的半径是1,则△ABC的斜边长为 .
问题解决
(2)小方的爸爸是一位翡翠设计师,一位顾客想将一块如图2所示的四边形原石BDFE进行切割设计.顾客首先需要切割出一个玉镯,再根据剩料进行其他设计.由于该原石成色最好的部分在∠B附近区域,所以玉镯要尽可能贴着BE边和BD边,观察到EF和DF的边缘都有杂质和细小裂隙,因此切割线不能经过DF边和EF边.根据原石情况和切割工艺,设计师需要先切割出能覆盖玉镯的三角形,再进行后期精细化打磨.为了最大限度地利用该石材,切割出的△ABC(点A在BD上,点C在BE上),应使得AC尽可能短,同时△ABC的周长和面积尽可能的小.经过测量,∠B=60°,BE=156mm,BD=175mm.根据顾客的需求,手镯的内圈直径为56mm,外圈直径为70mm,即小圆⊙O的直径为56mm,大圆⊙O的直径为70mm.
请你通过计算,帮助小方爸爸说明是否存在BD和BE上的点A和点C使得覆盖大圆⊙O的△ABC周长取得最小时,面积也取得最小值?若存在,请求出△ABC的周长及面积;若不存在,请说明理由.
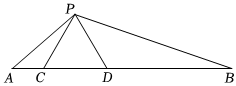 如图,点C,D在线段AB上,点P是线段AB外一点,满足△ACP∽△PDB.若△CPD是等腰直角三角形,∠CPD=90°,则∠APB的度数为( )
如图,点C,D在线段AB上,点P是线段AB外一点,满足△ACP∽△PDB.若△CPD是等腰直角三角形,∠CPD=90°,则∠APB的度数为( )
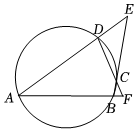 如图,圆内接四边形ABCD中,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,则∠A的度数为( )
如图,圆内接四边形ABCD中,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,则∠A的度数为( )

 如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.

