德优网2025陕西省西安市碑林区西工大附中初中数学考试期中七年级下
2024-2025学年陕西省西安市碑林区西北工大附中七年级(下)期中数学试卷
试卷总分:100分
命题人:dyczsxyn
考试时长:120分钟
一、选择题(8小题共24分)
1.
(本题3分)
化简2﹣1的结果是( )
A.2
B.﹣2
C..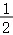
D.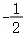
2.
(本题3分)
若在△ABC中,若∠A:∠B:∠C=2:3:5,则△ABC是( )
A.直角三角形
B.等腰三角形
C.锐角三角形
D.钝角三角形
3.
(本题3分)
截止2025年3月,我国已全面掌握14纳米芯片量产技术,7纳米工艺进入风险试产阶段.已知14纳米=0.000000014米,则数据0.000000014用科学记数法表示为( )
A.1.4×108
B.14×10-8
C.1.4×10-7
D.1.4×10-8
4.
(本题3分)
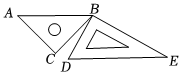 将一副三角板按如图所示方式放置于同一平面内,其中∠C=∠DBE=90°,∠A=45°,∠E=30°.若AB∥DE,则∠CBD的度数为( )
将一副三角板按如图所示方式放置于同一平面内,其中∠C=∠DBE=90°,∠A=45°,∠E=30°.若AB∥DE,则∠CBD的度数为( )
5.
(本题3分)
从﹣6,﹣2,0,3,6五个数中随机选一个数作为m的值,使得代数式x2﹣mx+9成为一个完全平方式的概率是( )
6.
(本题3分)
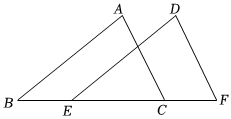 如图,点B,E,C,F在一条直线上,AB=DE,AB∥DE,要说明△ABC≌△DEF,则添加的条件不能是( )
如图,点B,E,C,F在一条直线上,AB=DE,AB∥DE,要说明△ABC≌△DEF,则添加的条件不能是( )
A.AC=DF
B.∠A=∠D
C.BE=CF
D.AC∥DF
7.
(本题3分)
数学课上,王老师与学生用如图所示的转盘做“用频率估计概率”的试验:随机转动转盘一次,当转盘停止后,指针指向阴影区域(若指向分界线,则重转)的频率如图所示,那么可以推算出所有阴影部分的圆心角之和大约是( )
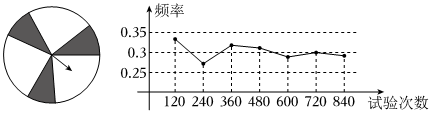
A.126°
B.108°
C.90°
D.72°
8.
(本题3分)
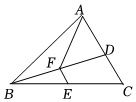 如图,已知点D、E分别为△ABC的边AC、BC的中点,AF为△ABD的中线.若四边形ACEF的面积为15,AB=6,则在△ABC中,AB边上的高为( )
如图,已知点D、E分别为△ABC的边AC、BC的中点,AF为△ABD的中线.若四边形ACEF的面积为15,AB=6,则在△ABC中,AB边上的高为( )
二、填空题(5小题共15分)
9.
(本题3分)
计算:2024×2026-20252= .
10.
(本题3分)
等腰三角形的两边分别4和9.则这个等腰三角形的周长为 .
11.
(本题3分)
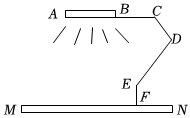 如图是一款长臂折叠LED护眼灯的示意图,EF与桌面MN垂直,当发光的灯管AB恰好与桌面MN平行时,∠DEF=140°,∠BCD=120°,则∠CDE的度数为 .
如图是一款长臂折叠LED护眼灯的示意图,EF与桌面MN垂直,当发光的灯管AB恰好与桌面MN平行时,∠DEF=140°,∠BCD=120°,则∠CDE的度数为 .
12.
(本题3分)
现有边长为a的正方形甲卡片,边长为b的正方形乙卡片,长和宽分别为a、b的长方形丙卡片若干张.如果用以上卡片拼成一个两边长分别为2a+b、a+3b的长方形,那么需要甲、乙、丙三类卡片的总张数为 .
13.
(本题3分)
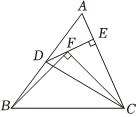 如图,在△ABC中,点D为AB边中点,DE⊥AC,垂足为E.以BC为斜边作等腰Rt△BFC,使得直角顶点F恰好在DE上.若AC=10,DF=2,则的值为 .
如图,在△ABC中,点D为AB边中点,DE⊥AC,垂足为E.以BC为斜边作等腰Rt△BFC,使得直角顶点F恰好在DE上.若AC=10,DF=2,则的值为 .
三、解答题(9小题共61分)
14.
(本题12分)
计算:
(1)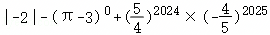 ;
;
(2)a2•a4﹣(2a3)2+a8÷a2;
(3)2m(m﹣1)﹣(2m3﹣m)÷m;
(4)(x﹣2y+3)(x+2y+3).
15.
(本题5分)
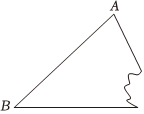 已知:破损的△ABC的一部分,请用尺规作图法,求作△DEF,使其与△ABC全等.(不写作法,保留作图痕迹)
已知:破损的△ABC的一部分,请用尺规作图法,求作△DEF,使其与△ABC全等.(不写作法,保留作图痕迹)
16.
(本题5分)
先化简,再求值:[(x+2y)2-(5x+y)(5x-y)-5y2]÷(-2x),其中x、y满足x2+y2-2x+6y+10=0.
17.
(本题5分)
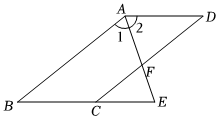 已知:如图,AD∥BC,∠B+∠BCD=180°,∠BAD的平分线交CD于点F,交BC的延长线于点E.
已知:如图,AD∥BC,∠B+∠BCD=180°,∠BAD的平分线交CD于点F,交BC的延长线于点E.
求证:∠CFE=∠E.
请将下面的证明过程补充完整:
证明:∵AD∥BC(已知),
∴∠2=∠E( ).
∵AE平分∠BAD(已知),
∴∠1=∠2(角平分线定义)
∴∠E=∠1( ).
又∵∠B+∠BCD=180°(已知),
∴AB∥ ( ).
∴∠1= (两直线平行,同位角相等).
∴∠CFE=∠E(等量代换).
18.
(本题5分)
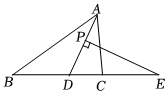 如图,AD为△ABC的角平分线,点P为AD上的点,过点P作PE⊥AD交BC的延长线于点E.若∠B=30°,∠ACB=80°,求∠E的度数.
如图,AD为△ABC的角平分线,点P为AD上的点,过点P作PE⊥AD交BC的延长线于点E.若∠B=30°,∠ACB=80°,求∠E的度数.
19.
(本题6分)
一个不透明的布袋中装有四个小球,球上分别标有数字3,3,4,5,它们除所标数字外其余均相同.
(1)从布袋中随机取出一个小球,取出小球上标有数字3的概率为 ;
(2)从布袋中随机取出一个小球,放回,摇匀后再随机取出一个小球,请用画树状图或列表的方法求两球所标数字之和为奇数的概率.
20.
(本题6分)
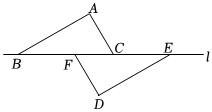 如图,点B,F,C,E在直线l上,AC∥DF,AB∥DE,AB=DE.
如图,点B,F,C,E在直线l上,AC∥DF,AB∥DE,AB=DE.
(1)求证:BF=CE;
(2)若∠A=100°,∠FED=30°,求∠BFD的度数.
21.
(本题7分)
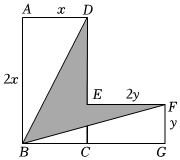 对于任意数a,b,c,d,我们规定(a,b)☆(c,d)=a2-bc+d2.
对于任意数a,b,c,d,我们规定(a,b)☆(c,d)=a2-bc+d2.
(1)计算(1,2)☆(3,-2)的结果为 ;
(2)对于数x,y,若x+y=8,(x,x)☆(y,y)=46.
①求xy的值;
②将长方形ABCD和长方形CEFG按照如图方式放置,点E在边CD上,连接BD,BF.若AB=2x,AD=x,EF=2y,FG=y,求图中阴影部分的面积.
22.
(本题10分)
问题探究
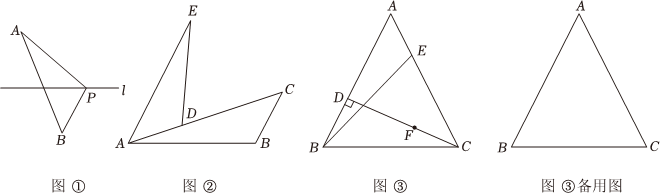
(1)如图①,在直线l的异侧有A,B两点,其距离为4.点P为直线l上的动点,则AP+BP的最小值为 ;
(2)如图②,已知△ABC边AC上有一点D,且满足AD=CB,过点A作AE∥BC,并截取AE=AC,连接ED,求证:ED=AB;
问题解决
(3)某村为了美化环境,准备在一块等腰三角形的空地上种植花卉,供居民观赏.等腰三角形空地为如图③所示的△ABC,其中CD为原本的一条小路,为种植不同种类的花卉及方便游人观赏,还需再开发两条小路BE和AF,其中点E,点F分别在AC,CD上,且满足AE=CF,为节约成本,要求两条小路的长度和最小,即BE+AF最小.已知在△ABC中,AB=AC,∠BAC=55°,CD⊥AB,垂足为点D.那么这样的设计要求能否达到?若能,求出当BE+AF最小时,∠AFD的度数;若不能,请说明理由.
转载声明:
本题解析属于发布者收集录入,如涉及版权请向平台申诉!
!版权申诉
 将一副三角板按如图所示方式放置于同一平面内,其中∠C=∠DBE=90°,∠A=45°,∠E=30°.若AB∥DE,则∠CBD的度数为( )
将一副三角板按如图所示方式放置于同一平面内,其中∠C=∠DBE=90°,∠A=45°,∠E=30°.若AB∥DE,则∠CBD的度数为( )
 如图,点B,E,C,F在一条直线上,AB=DE,AB∥DE,要说明△ABC≌△DEF,则添加的条件不能是( )
如图,点B,E,C,F在一条直线上,AB=DE,AB∥DE,要说明△ABC≌△DEF,则添加的条件不能是( )

 如图是一款长臂折叠LED护眼灯的示意图,EF与桌面MN垂直,当发光的灯管AB恰好与桌面MN平行时,∠DEF=140°,∠BCD=120°,则∠CDE的度数为 .
如图是一款长臂折叠LED护眼灯的示意图,EF与桌面MN垂直,当发光的灯管AB恰好与桌面MN平行时,∠DEF=140°,∠BCD=120°,则∠CDE的度数为 .
 已知:如图,AD∥BC,∠B+∠BCD=180°,∠BAD的平分线交CD于点F,交BC的延长线于点E.
已知:如图,AD∥BC,∠B+∠BCD=180°,∠BAD的平分线交CD于点F,交BC的延长线于点E. 如图,点B,F,C,E在直线l上,AC∥DF,AB∥DE,AB=DE.
如图,点B,F,C,E在直线l上,AC∥DF,AB∥DE,AB=DE. 对于任意数a,b,c,d,我们规定(a,b)☆(c,d)=a2-bc+d2.
对于任意数a,b,c,d,我们规定(a,b)☆(c,d)=a2-bc+d2.
