服务热线
搜题▪组卷
试卷总分:120分 命题人:dyczsxyn 考试时长:120分钟
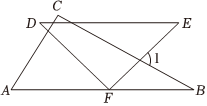如图，一副直角三角板如图所示摆放，∠B=30°，∠E=45°，若DE∥AB，则∠1的度数是（ ）
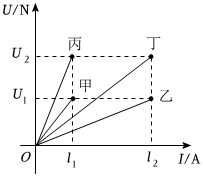物理实验中，同学们分别测量电路中经过甲、乙、丙、丁四个用电器的电流I（A）和它们两端的电压U（V），根据相关数据，在如图的坐标系中依次画出相应的图象．根据图象及物理学知识U=IR，可判断这四个用电器中电阻R（Ω）最大的是（ ）
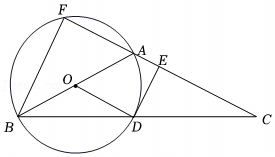
如图，四边形ABCD是⊙O的内接四边形，AB是⊙O的直径，若∠BEC=20°，则∠ADC的度数为（ ）
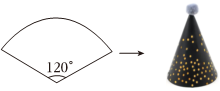在数学跨学科主题活动课上，芳芳用半径为15cm,圆心角为120°的扇形纸板，做了一个圆锥形的生日帽，如图所示，在不考虑接缝的情况下，这个圆锥形生日帽的底面圆的半径是 cm.
，反比例函数
的图象经过点B，则k的值为 ．
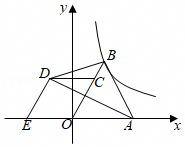
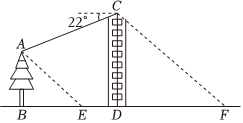如图，小知想测量自家小区居民楼下一棵大树AB的高度，由于大树旁边还有其他灌木无法直接到达大树下面测量，他先通过查询建筑说明得到居民楼CD的高度为28m,接着在居民楼CD的顶端C处测得大树的顶端A的俯角为22°，某一时刻在太阳光的照射下，大树AB顶端A的影子落在地面上的点E处，居民楼CD顶端C的影子落在地面上的点F处，测得DE=10m,DF=30.8m,已知大树和居民楼均垂直于地面，且点B，E，D，F在同一条直线上，求大树的高度AB．（结果精确到0.1m,参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40）
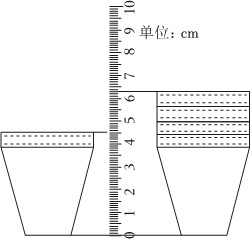如图，1个和4个叠在一起的杯子放在刻度尺的两侧，刻度尺的0刻度线与两叠杯子底面平齐，左右两叠杯子上边缘对应刻度尺上的读数分别是4.5和6.3．| 分组 | 个数x | 频数（人数） | 每组仰卧起坐的平均个数/个 |
| A | 10≤x＜20 | 8 | 15 |
| B | 20≤x＜30 | 18 | 26 |
| C | 30≤x＜40 | n | 34 |
| D | 40≤x≤50 | 8 | 46 |
，求CF的长．
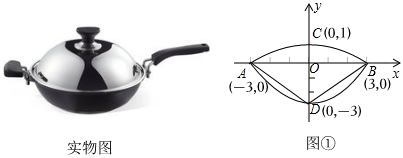我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两段抛物线组合而成封闭图形，不妨简称为“锅线”，锅口直径为6dm,锅深3dm,锅盖高1dm（锅口直径与锅盖直径视为相同），建立直角坐标系如图①所示，如果把锅纵断面的抛物线记为C1，把锅盖纵断面的抛物线记为C2．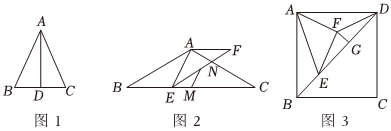
gl@dyw.com
2025-03-24
初中数学 | 模考 | 难度:1.96
| 下载试卷 | 收藏 |
| 平行组卷 | 细目重组 |
| 试卷分析 | 加入白板 |
| 加卷篮 | 更多功能 |
平行组卷卷生成中,请等待
解析
纠错
收藏
下载
相似
组卷
如图，在△ABC中，∠B=90°，AB=6，将△ABC沿着BC的方向平移至△DEF，若四边形ADFC的面积为24，则平移的距离为 ．
如图，在Rt△ABC中，∠ACB=90°，CA=CB=3，线段CD绕点C在平面内旋转，连接AD，过点B作AD的垂线，交射线AD于点E．若CD=1，则AE的最大值为 ．
如图所示，在四边形ABCD中，CD∥AB，点E在AC上，且BE=AD，∠ABE=∠CAD．求证：AE=CD．