服务热线
搜题▪组卷
m，
，∠ABC＝45°，AD＝CD，∠ADC＝90°，弧ABC为⊙O上的一段优弧，点E为弧BC上的一点，过点E与点O铺设一条观赏小路EF，过点A铺设一条与之垂直的观赏小路AF，垂足为F，现计划在△FCD内种植牡丹花，已知牡丹花每平米的成本费为500元，则种植牡丹花所需费用至少为多少元？
，
；
，
，
，
；
，
；
，
，
，
，
，
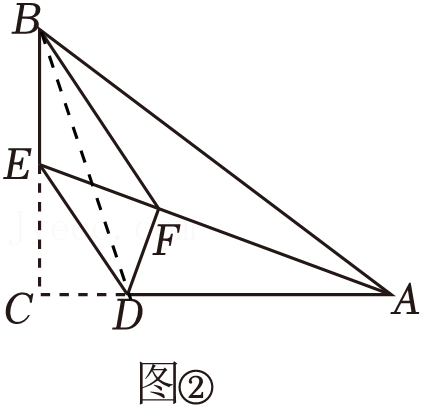
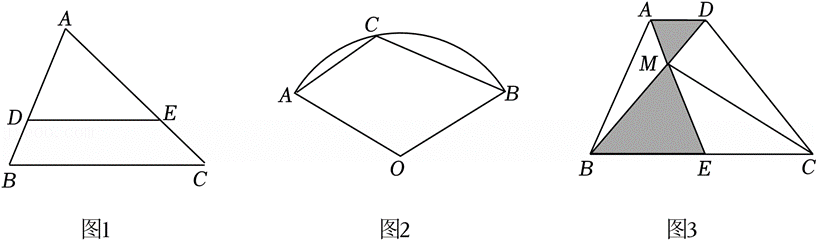
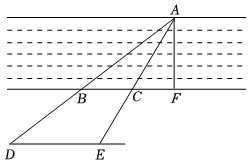为了保障市民出行方便，某市在流经该市的河流上架起一座桥，小明和小颖想通过自己所学的数学知识计算该桥AF的长．如图，该桥两侧河岸平行，他们在河的对岸选定一个目标作为点A，再在河岸的这一边选出点B和点C，分别在AB、AC的延长线上取点D、E，使得DE∥BC．经测量，BC=80米，DE=140米，且点E到河岸BC的距离为75米．已知AF⊥BC于点F，请你根据提供的数据帮助他们计算桥AF的长度．
上一动点，连接AB，MP，AB与MP相交于点Q，若
，BM＝9，求PQ的最大值；【问题解决】
，点D是BC边上一动点，DE⊥AB于点E，DF⊥AC于点F，⊙O是四边形AEDF的外接圆，求⊙O直径的最小值．
米，AB＝400
米，点E在CD上，且CE＝2DE，F、G分别是边AB、BC上的两个动点，且∠FEG＝60°．为了改善人居环境，小区物业准备在尽可能大的四边形BFEG区域内种植花卉，请问这个四边形BFEG区域的面积是否存在最大值？若存在，求出面积的最大值；若不存在，请说明理由．
时，求PB+PC的最小值；
米，赵老师准备在△ABP内种植当季蔬菜，边BE的中点F为菜园出入口，为了种植方便，她打算在AE边上取点M，并沿PM、MF修两条人行走道，要求人行走道的总长度尽可能小，问PM+MF的长度是否存在最小值？若存在，求出其最小值；若不存在，请说明理由．
综合与实践
，求CF的长．
，AD＝6．点P是圆心角为120°的圆弧AD上的一点，点E在BC边上，且BE＝1．连接EP，求EP的最大值．
，求AD的长．
，连接BP，将BP绕点B逆时针旋转90°至BF，连接AF，问是否存在F使得△CDF的面积最大？若存在，请求出△CDF面积的最大值；若不存在，请说明理由．
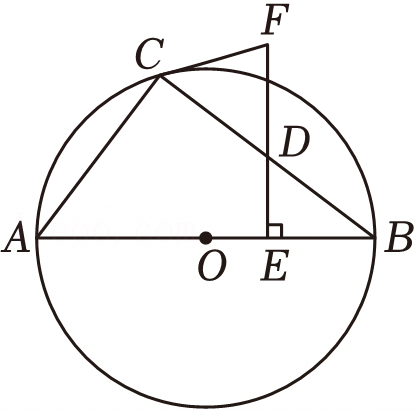
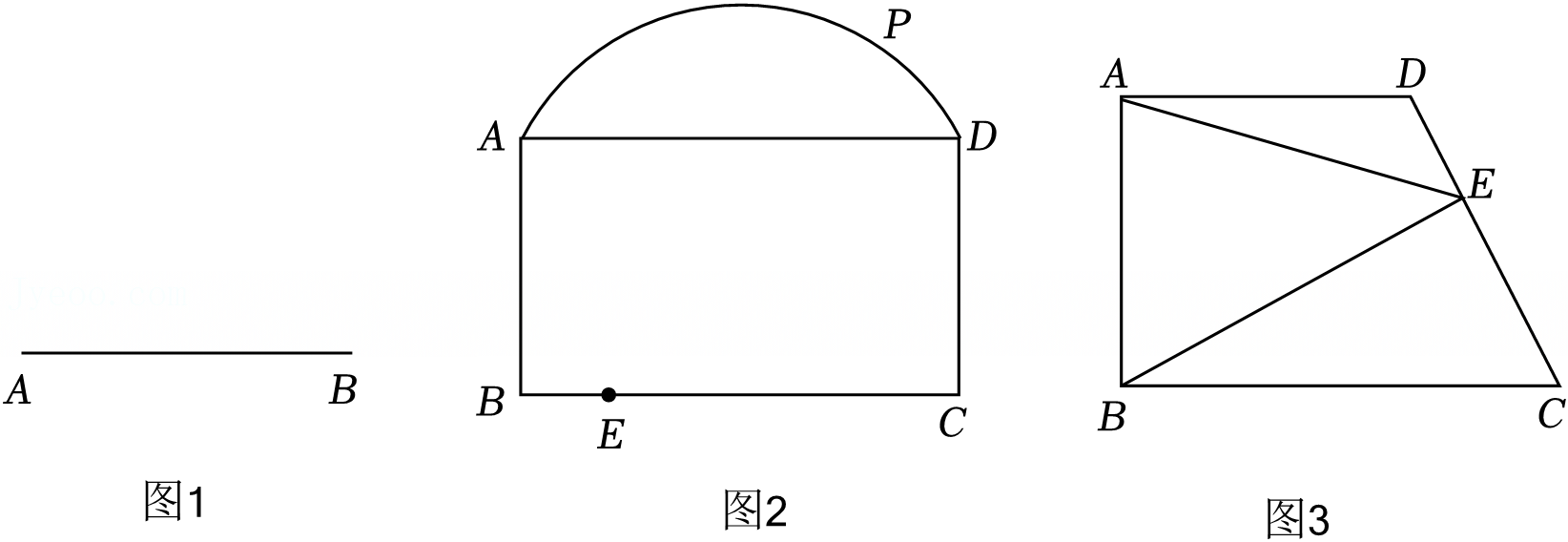
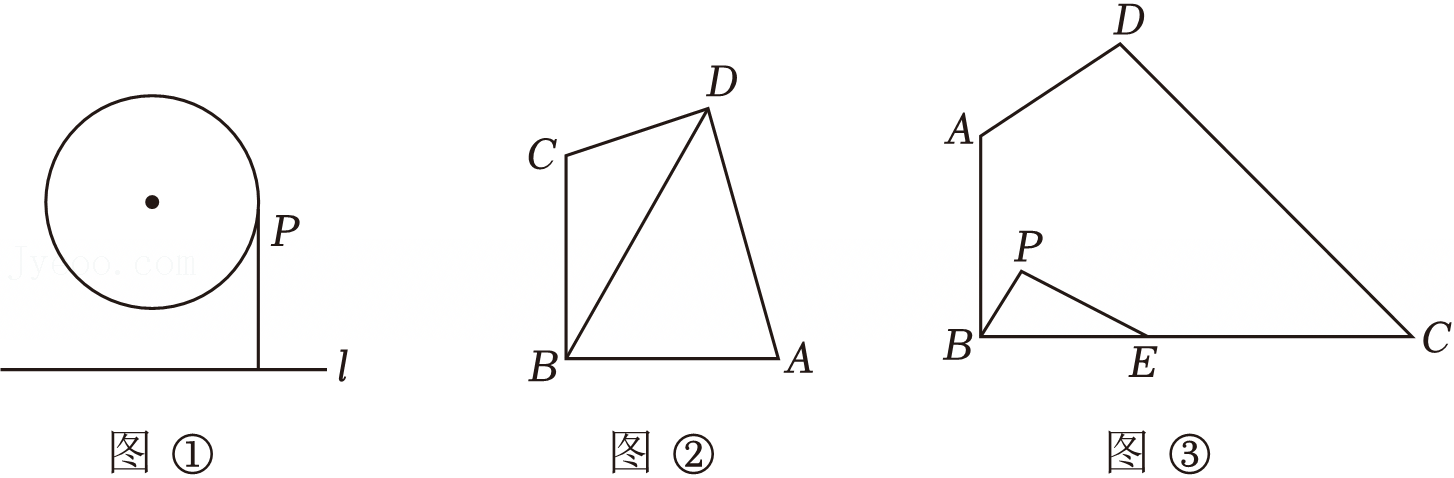
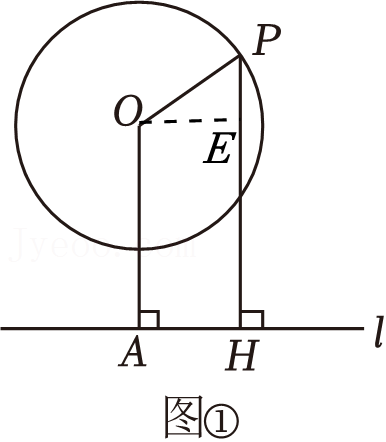
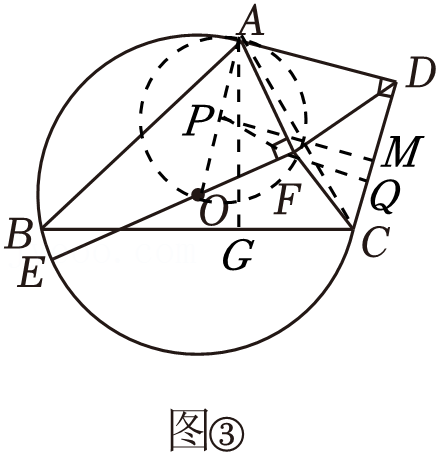
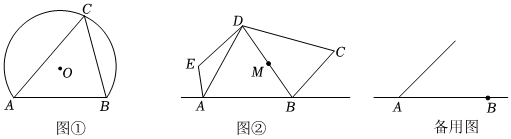
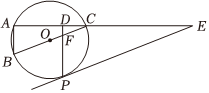如图，△ABC内接于⊙O，BC是⊙O的直径，点P是⊙O上一点，过点P作⊙O的切线PE交AC的延长线于点E，过点P作PD⊥AC于点D，交BC于点F，∠B=∠DPE．
，∠AOB＝120°，点C是
上一点，则△ABC面积的最大值为 ；
上的一动点，连接AC，BC，∠AOB＝120°，OA＝2，求四边形OACB的面积的最大值．
．为倡导绿色新风尚，现要使绿化的面积尽可能的大，请问△MBE和△MDA的面积之和是否存在最大值？若存在，请求出△MBE和△MDA的面积之和的最大值；若不存在，请说明理由．
czy@dyw.com
2024-04-24
初中数学 | 九年级下 | 解答题
纠错
收藏
下载
相似
组卷
解析
