[考点]
垂线段最短,等腰三角形的判定与性质,等边三角形的判定,含30度角的直角三角形,全等三角形的判定与性质,
[答案]
(1)AC⊥BD;BE=DE;
(2)①证明见解析;②点H的位置见解析,CH=2GH.
[解析]
(1)解:AC与BD的位置关系为:AC⊥BD;BE与DE的数量关系为:BE=DE.
理由:∵∠ABD=∠ADB,
∴AB=AD,
∵∠ABC=∠ADC=90°,
∴△ABC和△ADC都是直角三角形,
在Rt△ABC和Rt△ADC中,
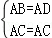 ,
∴Rt△ABC≌Rt△ADC(HL),
∴CB=CD,
∴AC垂直平分BD,
∴AC⊥BD,BE=DE,
故答案为:AC⊥BD;BE=DE;
(2)①证明:如图,设∠F=α,
∵AB=AF,
∴∠ABF=∠F=α,
∵∠BAC是△ABF的外角,
∴∠BAC=∠F+∠ABF=α+α=2α,
由(1)知,AC⊥BD,CB=CD,
∴∠BCE=∠DCE,
∵BF∥CD,
∴∠DCE=∠F=α,
∴∠BCE=∠DCE=α,
∵∠ABC=90°,
∴∠BCE+∠BAC=90°,即α+2α=90°,
解得:α=30°,
∴∠DCB=2∠BCE=60°,
∵CB=CD,
∴△BCD是等边三角形;
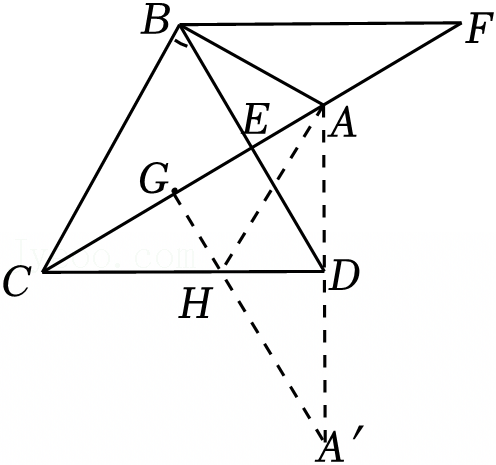
②解:如图,延长AD至点A′,使DA′=DA,
∵CD⊥AD,
∴点A与点A′关于直线CD轴对称,过点A′作A′G⊥AC于点G,交CD于点H,连接AH,
∴AH=A′H,
∴AH+GH=A′H+GH=A′G,此时GH+AH的值最小,
由①知,∠DCE=30°,即∠GCH=30°,
∵A′G⊥AC,即GH⊥CG,
∴在Rt△GCH中,∠GCH=30°,
∴CH=2GH,
∴当GH+AH的值最小时,点H的位置如图所示,GH与CH的数量关系是CH=2GH.
,
∴Rt△ABC≌Rt△ADC(HL),
∴CB=CD,
∴AC垂直平分BD,
∴AC⊥BD,BE=DE,
故答案为:AC⊥BD;BE=DE;
(2)①证明:如图,设∠F=α,
∵AB=AF,
∴∠ABF=∠F=α,
∵∠BAC是△ABF的外角,
∴∠BAC=∠F+∠ABF=α+α=2α,
由(1)知,AC⊥BD,CB=CD,
∴∠BCE=∠DCE,
∵BF∥CD,
∴∠DCE=∠F=α,
∴∠BCE=∠DCE=α,
∵∠ABC=90°,
∴∠BCE+∠BAC=90°,即α+2α=90°,
解得:α=30°,
∴∠DCB=2∠BCE=60°,
∵CB=CD,
∴△BCD是等边三角形;
②解:如图,延长AD至点A′,使DA′=DA,
∵CD⊥AD,
∴点A与点A′关于直线CD轴对称,过点A′作A′G⊥AC于点G,交CD于点H,连接AH,
∴AH=A′H,
∴AH+GH=A′H+GH=A′G,此时GH+AH的值最小,
由①知,∠DCE=30°,即∠GCH=30°,
∵A′G⊥AC,即GH⊥CG,
∴在Rt△GCH中,∠GCH=30°,
∴CH=2GH,
∴当GH+AH的值最小时,点H的位置如图所示,GH与CH的数量关系是CH=2GH.
[点评]
本题考查了"垂线段最短,等腰三角形的判定与性质,等边三角形的判定,含30度角的直角三角形,全等三角形的判定与性质,",属于"压轴题",熟悉题型是解题的关键。
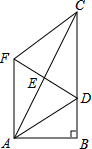
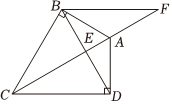 如图,在四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点E,∠ABD=∠ADB.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点E,∠ABD=∠ADB.