服务热线
搜题▪组卷
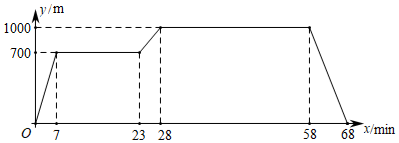
| 离开教学楼的时间/min | 2 | 20 | 25 | 30 |
| 离教学楼的距离/m | 700 |
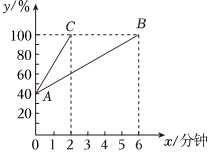用充电器给某手机充电时，其屏幕画面显示目前电量为40%．经测试，在用快速充电器和普通充电器对该手机充电时，其电量y（单位：%）与充电时间x（单位：分钟）的函数图象分别为图中的线段AC，AB．
某医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用后，每毫升血液中含药量y（微克）随时间x（时）的变化情况如图所示，根据图象回答下列问题：| x（厘米） | 1 | 2 | 4 | 7 | 11 | 12 |
| y（斤） | 0.75 | 1.00 | 1.50 | 2.75 | 3.25 | 3.50 |
西安是一个历史悠久风景美丽的城市．已经结束的2022年西安国际马拉松比赛，从赛道两旁的美景到热情的古城人民都给大家留下了美好的回忆．为了积极准备2023年西安国际马拉松比赛，小明和小亮相约周末去曲江池锻炼．他们计划沿着曲江池跑两圈，已知曲江池一圈路程为4.2km,他们从同一地点出发，小亮先跑，他们的锻炼过程如图所示，横轴表示跑步时间，纵轴表示路程，请根据图中信息回答下列问题．
某市为节约水资源，制定了新的居民用水收费标准．按照新标准，用户每月缴纳的水费y（元）与每月用水量x（m3）之间的关系如图所示．
今年，由于新冠肺炎的爆发，市场对口罩的需求量急剧增大．某口罩生产商自二月份以来，一直积极恢复产能，每日口罩生产量y（百万个）与天数x（x为正整数）的函数关系图象如图所示．而该生产商对口供应市场对口罩的需求量不断上升，且每日需求量z（百万个）与天数x满足一次函数关系．已知第1天需求1500万个口罩，第6天需求2000万个口罩．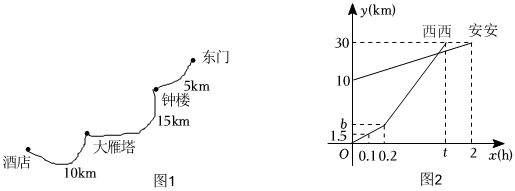
| 运力（箱/辆） | 租金（元/辆） | |
| 大货车 | 45 | 400 |
| 小货车 | 35 | 320 |
已知A、B两地之间有一条270千米的公路，甲、乙两车同时出发，甲车以60千米/时的速度沿此公路从A地匀速开往B地，乙车从B地沿此公路匀速开往A地，两车分别到达目的地后停止．甲、乙两车相距的路程y（千米）与甲车的行驶时间x（时）之间的函数关系如图所示．
dycs2021
2021-04-29
初中数学 | 七年级下 | 解答题
纠错
收藏
下载
相似
组卷
解析
