阅读理解定义为数轴上三点若点到点的距离是它到点的距离的倍是大于的正整数则称点是的倍点例如在图中点是的倍点若图中点是的倍点填或若如图为数轴上两个点点表示的数是点表示的数是点是的倍点则点表示的数是图中一动点从出发沿数轴向右运动若恰好是的倍点求点走过的路程是多少单位长度用含的式子表示

首页 > 试题列表 > 单题解析

198361. （2022•爱知中学•七上期中）阅读理解：
定义：A，B，C为数轴上三点，若点C到点A的距离是它到点B的距离的n倍（n是大于1的正整数），则称点C是A，B的n倍点．例如：在图1中，点C是AB的2倍点．
$德优题库$
（1）若n=2，图1中，点是C，D的2倍点．（填A或B）
（2）若n=3，如图2，M，N为数轴上两个点．点M表示的数是-2，点N表示的数是4，点P是M，N的3倍点，则点P表示的数是．
（3）图2中，一动点P从M出发，沿数轴向右运动，若P恰好是MN的n倍点，求点P走过的路程是多少单位长度．（用含n的式子表示）

共享时间:2022-11-10 难度:2

纠错

下载

相似

组卷白板

[考点]

数轴，列代数式，

[答案]

（1）A；

（2）7或2.5或﹣0.5或﹣5；

（3）m＝

或

．

[解析]

解：（1）当n＝2时，则点A为﹣1，点C为1，点D为0，
则AC＝1﹣（﹣1）＝2，AD＝0﹣（﹣1）＝1，
满足AC＝2AD，
故A是C、D的2倍点，
故答案为：A；
（2）当n＝3时，则点M表示的数是﹣2，点N表示的数是4，
设点P表示的数为p，
则PM＝

，PN＝

，
若点P是M，N的3倍点，
则PM＝3PN或PN＝3PM，
∴

＝3

或3

＝

，
解得：p＝7或2.5或﹣0.5或﹣5；
故答案为：7或2.5或﹣0.5或﹣5；
（3）一动点P从M：﹣2出发，沿数轴向右运动，
设向右走m各单位长度，（m＞0），
则此时P表示的数为：﹣2+m，
∵N表示的数是4，
∴PM＝﹣2+m﹣（﹣2）＝m，PN＝

＝

，
若点P是M，N的n倍点，
则PM＝nPN或PN＝nPM，
∴m＝n

或nm＝

，
∴m＝±n（m﹣6）或mn＝±（m﹣6），
∴m＝

或

（舍去）或

，
∴m＝

或

．

[点评]

本题考查了"数轴，列代数式，"，属于"必考题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

82692. （2024•铁一中学•七上期末）（1）基础回顾：数轴上表示有理数1和5的两点之间的距离是        ；表示有理数-3和5两点之间的距离是        ．
（2）新定义：一般的，在数轴上有一个点A，另一个点B到这个点的距离叫做栋梁距离，则点B叫做点A在该栋梁距离时的求知点，点B对应的数叫做求知数．例如，数轴上表示2的点，在栋梁距离为3时对应的求知数为-1和5，在栋梁距离为1时对应的求知数为1和3，在栋梁距离为0时对应的求知数是2．
请根据定义回答下列问题：
①数轴上表示有理数3的点在栋梁距离为1时对应的求知数是        ．
②数轴上表示有理数-1的点在栋梁距离为0时对应的求知数是        ．
学以致用：
③在数轴上，点A是点C在栋梁距离为m时的求知点，有理数m对应的点是点B在栋梁距离为6时的求知点，是否存在唯一的点B，使得对于数轴上每一个确定的点C，数轴上有且只有三个点A满足条件？若存在，求出点B对应的数；若不存在，请说明理由．
④若将③中的语句改成：在数轴上，点A与点C的距离为m,点B与有理数m对应的点的距离为6，是否存在唯一的点B，使得对于数轴上每一个确定的点C，数轴上有且只有三个点A满足条件？若存在，求出点B对应的数；若不存在，请说明理由．请问，③的结论        .（填一定成立或不一定成立或一定不成立）

共享时间:2024-02-13 难度:3 相似度:1.67

解析

纠错

下载

组卷白板

172844. （2024•逸翠园中学•七上一月）我们知道：如果A、B两点在数轴上对应的数分别为x₁、x₂，那么AB之间的距离可以表示为：|AB＝|x₁﹣x₂|；若C为线段AB的中点，则点C在数轴上对应的数x可以表示为：

．
如图，O点是数轴上的原点，M、N是数轴上的两个点，M点对应的数是为﹣4，N点对应的数是为6．

（1）若M以每秒2个单位的速度向右运动，N以每秒4个单位的速度向左运动，求　1　秒后O为MN的中点．
（2）若M、N两个点同时出发沿着数轴运动．点M向右运动，点N向左运动，3秒后它们之间的距离为1个单位长度，且N的速度是M的两倍，分别求M、N的速度；
（3）我们规定，在数轴上，当A、B两点都位于原点的右侧且其中一个点到原点的距离是另一个到原点的距离1.5倍：或当A、B两点都位于原点左侧且两个点到原点的距离都相等时，这两种情况均称为AB两点是“相见恨晚距离”．若动点P从原点出发，以每秒1个单位的速度向左运动到点M后原速返回到点N后停止运动，同时，动点Q从点N出发，以每秒2个单位的速度向左在M、N之间作往返运动，且当点P停止运动时，动点Q也之停止运动，求所有满足条件的PQ两点是“相见恨晚距离”的时间？

共享时间:2024-10-10 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

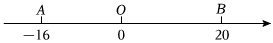173958. （2024•西工大附中•七上一月） $德优题库$ 如图，已知数轴上有A、B两点，点A表示的数是-16，点B表示的数是20，动点P、Q分别从A、B两点同时出发，在数轴上匀速相向而行，它们的速度分别为1个单位长度/秒、2个单位长度/秒，设运动时间为t.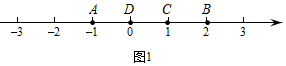
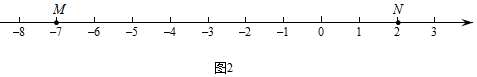
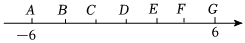（1）当t=1时，点P对应的数是，点Q对应的数是；
（2）当t为何值时，P、Q两点之间相距8个单位长度；
（3）当t=2时，若线段AP和线段QB同时以1个单位长度/秒的速度同时相向匀速运动，是否存在某一时刻？使得AQ+PB=18．若存在，求出此时PQ的距离，若不存在，请说明理由．

共享时间:2024-10-13 难度:4 相似度:1.5

解析

纠错

下载

组卷白板

172742. （2024•远东二中•七上一月）邮递员骑车从邮局出发，先向西骑行2km到达A村，继续向西骑行3km到达B村，然后向东骑行8km，到达C村，最后回到邮局．
（1）以邮局为原点，以向东方向为正方向，用1cm表示1km，画出数轴，并在该数轴上表示出A，B，C三个村庄的位置；
（2）C村距离A村有多远？
（3）邮递员共骑行了多少km？

共享时间:2024-10-16 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

173109. （2024•高新三中•七上一月）定义：若A，B，C为数轴上三点，若点C到点A的距离是点C到点B的距离2倍，我们就称点C是【A，B】的美好点．
例如：如图1，点A表示的数为-1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是【A，B】的美好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是【A，B】的美好点，但点D是【B，A】的美好点．
$德优题库$
如图2，M，N为数轴上两点，点M所表示的数为-7，点N所表示的数为2．
$德优题库$
（1）点E，F，G表示的数分别是-3，6.5，11，其中是【M，N】美好点的是；写出【N，M】美好点H所表示的数是．
（2）现有一只电子蚂蚁P从点N开始出发，以2个单位每秒的速度向左运动．当t为何值时，P，M和N中恰有一个点为其余两点的美好点？
$德优题库$

共享时间:2024-10-22 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

173933. （2024•高陵区•七上一月） $德优题库$ 如图，数轴上标出的所有点中，任意相邻两点间的距离都相等，已知点A表示的数是-6，点G表示的数是6．
（1）表示原点的是点，点C表示的数是；
（2）在点D的右侧有两点P、Q，点P到点C的距离是3；点Q到点E的距离是6，则点P，Q之间的距离是多少？

共享时间:2024-10-29 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

25273. （2023•高新一中•八下期中）八年级某班同学原来计划租一辆大巴车去研学，大巴车的租价为800元，实际又增加了3名同学，租车价不变，若设原来计划参加研学的同学共有x人，实际每个同学比原来少分摊车费元．

共享时间:2022-05-29 难度:2 相似度:1.5

解析

纠错

下载

组卷白板

172743. （2024•远东二中•七上一月）如图，已知数轴上点A表示的数为6，且AB＝10，动点P从点A出发，以每秒2个单位长度的速度沿数轴向左匀速运动．设运动时间为t秒（t＞0）．

（1）数轴上点B表示的数为　﹣4　．当t＝2时，点P表示的数为　2　；
（2）动点R从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P，R同时出发，问经过多长时间P，R两点相遇？
（3）动点R从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P，R同时出发，问点R运动多长时间P，R两点相距2个单位长度？

共享时间:2024-10-16 难度:2 相似度:1

解析

纠错

下载

组卷白板

172837. （2024•逸翠园中学•七上一月）把下列各数表示在数轴上，并用“＜”把它们连接起来．
﹣4，﹣|﹣2|，

，

．

共享时间:2024-10-10 难度:2 相似度:1

解析

纠错

下载

组卷白板

23040. （2021•铁一中学•七上期中）为使课后服务更加丰富多彩，某学校准备在网上订购一批某品牌羽毛球拍和羽毛球开设羽毛球课，经查阅发现羽毛球拍一副定价40元，羽毛球每个定价5元，“双十一”期间A、B两家网店均提供包邮服务，并给出了各自的优惠方案．
A网店：买一副球拍送2个羽毛球；B网店：羽毛球拍和羽毛球都按定价的80%付款．已知要购买羽毛球拍30副，羽毛球x个（x＞60）；
（1）若在A网店购买，需付款　　元（用含x的代数式表示）；若在B网店购买，需付款　　元（有含x的代数式表示）．
（2）若x＝70时，通过计算说明哪家网店购买较为合算？

共享时间:2021-11-22 难度:4 相似度:1

解析

纠错

下载

组卷白板

172637. （2024•长安区•月考）某检修小组开车从单位出发，检修东西走向的供电线路，规定向东为正，向西为负，一天的行程是（单位：千米）：+15，-3，+16，-11，+10，-2，4，-15，16，-18．
（1）最后他们是否回到出发点？若没有，则在出发点的什么方向？距离出发点多远？
（2）若汽车耗油量为0.6升/千米，检修小组完成工作返回出发地，则他们该天共耗油多少升？

共享时间:2023-12-01 难度:2 相似度:1

解析

纠错

下载

组卷白板

173157. （2024•高新二中•七上一月）已知数轴上三点M，O，N对应的数分别为-1，0，3，点P为数轴上任意一点，共对应的数为x. $德优题库$
（1）MN的长为；
（2）如果点P到点M、点N的距离相等，那么x的值是；
（3）如果点P以每分钟1个单位长度的速度从点O向左运动，同时点M和点N分别以分钟2个单位长度和每分钟3个单位长度的速度也向左运动，设t分钟时点P到点M、点N的距离相等，求t的值．

共享时间:2024-10-10 难度:2 相似度:1

解析

纠错

下载

组卷白板

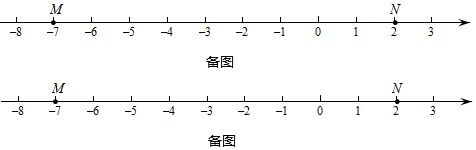
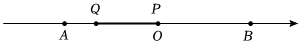173239. （2024•西光中学•七上二月） $德优题库$ 在数轴上互不重合的四个点A，B，M，N，如果MA=2NB或MB=2NA，那么点M，N叫做A，B两点的“2伴点”．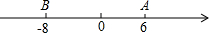
已知点A，B在数轴上表示的数分别为a,b,且满足|a+b|+|b-4|=0．
（1）填空：a= ，b= ；
（2）若点M表示的数为2，点N在原点右侧，且点M，N为点A，B的“2伴点”，求点N表示的数；
（3）如图，已知点O表示的数是0，把一根长为3个单位长度的木条PQ放在数轴上（点Q在点P的左侧），使得点P与点O重合．木条PQ以每秒2个单位长度的速度沿数轴匀速向右运动，当木条全部驶出线段OB时，速度变为原来的一半，设木条运动时间为t.当点P，Q为点A，B的“2伴点”时，求满足条件的所有t的值．

共享时间:2024-12-24 难度:2 相似度:1

解析

纠错

下载

组卷白板

173264. （2024•西光中学•七上一月）如图，已知数轴上两点A、B对应的数分别是6，-8，M、N、P为数轴上三个动点，点M从A点出发的速度为每秒2个单位，点N从点B出发的速度为M点的3倍，点P从原点出发的速度为每秒1个单位．
（1）若点M向右运动，同时点N向左运动，求多长时间点M与点N相距54个单位？
（2）若点M、N、P同时都向右运动，求多长时间点P到点M，N的距离相等？
$德优题库$

共享时间:2024-10-20 难度:2 相似度:1

解析

纠错

下载

组卷白板

27600. （2024•铁一中学•七上一月）结合数轴与绝对值的知识回答下列问题：
一般地，数轴上表示数m和数n的两点之间的距离公式为|m﹣n|．
（1）例如：数轴上表示4和1的两点之间的距离为|4﹣1|＝　   　
数轴表示5和﹣2的两点之间的距离为|5﹣（﹣2）|＝|5+2|＝　   　
（2）数轴上表示数a的点与表示﹣4的点之间的距离表示为　        　
数轴上表示数a的点与表示2的点之间的距离表示为　        　
若数轴上a位于﹣4与2之间，求|a+4|+|a﹣2|的值；
（3）当a＝　   　时，|a+5|+|a﹣1|+|a﹣4|的值最小，最小值为　   　．

共享时间:2024-10-21 难度:2 相似度:1

解析

纠错

下载

组卷白板

gl@dyw.com

2022-11-10

初中数学 | 七年级上 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2022-2023学年陕西省西安市新城区爱知中学七年级（上）期中数学试卷

更新:2022-11-10 12:08浏览量:27

微信扫码立即登录

AI助手

普通登录

手机登录

微信扫码立即登录

AI助手