首页 | 客服 | 上传赚现
AI助手
德优题库AI助手

AI助手

搜题▪组卷

计算题
1道
设置组卷 进入组卷
初中数学
同步组卷 细目组卷 错题组卷 试卷组卷 中考组卷 试卷中心 共享课件 共享练考 共享学校
(1)
设置组卷 进入组卷

服务热线

400-816-0029

    自建题库，共享分红

德优题库QQ交流群

首页 > 试题列表 > 单题解析
179783. （2025•交大附中•七下期中） 把代数式通过配方等手段得到完全平方式，再运用完全平方式的非负性这一性质解决问题，这种解题方法叫做配方法．配方法在代数式求值、解方程、最值问题等都有广泛的应用．如利用配方法，求a2+6a+8的最小值．
解：a2+6a+8=a2+6a+32-32+8=（a+3）2-1，因为不论a取何值，（a+3）2总是非负数，即（a+3）2≥0，所以当a=-3时，（a+3）2取最小值0，（a+3）2-1有最小值-1．
即当a=-3时，a2+6a+8有最小值-1．
根据上述材料，解答下列问题：
（1）将x2-10x+27变形为（x-m）2+n的形式       ，则x2-10x+27的最小值为       ；
（2）如果A-B＜0，则A＜B；如果A-B=0，则A=B；如果A-B＞0，则A＞B．
已知A=2x2-3x+2，B=x2-x-1，请比较A与B的大小，并说明理由；
（3）已知a2+b2-6a-14b+58=0，求2a-b的值．
共享时间:2025-05-12 难度:5
纠错 收藏 下载 相似 组卷 白板
[考点]
非负数的性质：偶次方，代数式求值，整式的加减，配方法的应用，不等式的性质，
[答案]
（1）（x﹣5）2+2；2；（2）A＞B；（3）﹣1．
[解析]
解：（1）由题意得，x2﹣10x+27＝（x﹣5）2+2．
又∵对于任意实数x满足（x﹣5）2≥0，
∴x2﹣10x+27＝（x﹣5）2+2≥2．
∴x2﹣10x+27的最小值为2．
故答案为：（x﹣5）2+2；2．
（2）由题意得，A﹣B＝（2x2﹣3x+2）﹣（x2﹣x﹣1）
＝2x2﹣3x+2﹣x2+x+1
＝x2﹣2x+1+2
＝（x﹣1）2+2．
∵对于任意实数x满足（x﹣1）2≥0，
∴A﹣B＝（x﹣1）2+2≥2＞0．
∴A＞B．
（3）由题意，∵a2+b2﹣6a﹣14b+58＝0，
∴a2﹣6a+9+b2﹣14b+49＝0．
∴（a﹣3）2+（b﹣7）2＝0．
∴a﹣3＝0，b﹣7＝0．
∴a＝3，b＝7．
∴2a﹣b＝2×3﹣7＝﹣1．
[点评]
本题考查了"非负数的性质：偶次方，代数式求值，整式的加减，配方法的应用，不等式的性质，"，属于"压轴题"，熟悉题型是解题的关键。
转载声明：
本题解析属于发布者收集录入，如涉及版权请向平台申诉！ ！版权申诉
181445. （2024•铁一中学•七下一月） 阅读下列材料：
a2±2ab+b2=（a±b）2，我们把形如“a2+2ab+b2”或“a2-2ab+b2”的多项式叫做完全平方式，因为（a±b）2是一个数的平方，具有非负性，我们常利用这一性质解决问题，这种解次问题的思路方法叫做配方法．用配方法解决下列问题：
（1）4992=（500-1）2=250000+       +1．
（2）当a,b为何值时，多项式a2+b2-4a+6b+18有最小值，并求出这个最小值．
（3）已知a,b,c为△ABC的三边长，且满足a2+2b2+c2-2b（a+c）=0，试判断此三角形的形状．
共享时间:2024-04-18 难度:2 相似度:1.4
解析 纠错 收藏 下载 组卷 白板
82689. （2024•铁一中学•七上期末） 已知x2-xy=2，2xy-y2=-3，求代数式2x2+4xy-3y2的值．
共享时间:2024-02-13 难度:2 相似度:1.4
解析 纠错 收藏 下载 组卷 白板
181314. （2024•未央区•七下二月） 已知a+b=7，ab=12，求a2+b2的值．
共享时间:2024-06-18 难度:1 相似度:1.2
解析 纠错 收藏 下载 组卷 白板
180144. （2024•长安区•八下二月） 根据不等式的性质，把下列不等式化为“x＞a”或“x＜a”的形式（a为常数）．
（1）5x﹣1＜﹣6；
（2）＞﹣1．
共享时间:2024-06-21 难度:1 相似度:1.2
解析 纠错 收藏 下载 组卷 白板
181034. （2024•西光中学•八下一月） 阅读材料：教科书中提到a2+2ab+b2和a2-2ab+b2这样的式子叫做完全平方式．”有些多项式不是完全平方式，我们可以通过添加项，凑成完全平方式，再减去这个添加项，使整个式子的值不变，这样也可以将多项式进行分解，并解决一些最值问题．
例如：分解因式：
x2-2x-3=x2-2x+1-4=（x-1）2-22=（x-1+2）（x-1-2）=（x+1）（x-3）
求代数式x2-2x-3的最小值
x2-2x-3=x2-2x+1-4=（x-1）2-4
（x-1）2≥0，∴当x=1时，代数式有x2-2x-3最小值-4．
结合以上材料解决下面的问题：
（1）分解因式x2+4x-5；
（2）求代数式x2+4x-5的最小值；
（3）当a、b为何值时，a2-2ab+2b2+4b+2024有最小值？最小值是多少？
共享时间:2024-04-22 难度:1 相似度:1.2
解析 纠错 收藏 下载 组卷 白板
25105. （2022•铁一中学•八下期中） 阅读下面材料，在代数式中，我们把一个二次多项式化为一个完全平方式与一个常数的和的方法叫做配方法，配方法是一种重要的解决问题的数学方法，它不仅可以将一个看似不能分解的多项式因式分解，还能求代数式最大值，最小值等问题．
例如：求代数式：x2-12x+2020的最小值．
解：原式=x2-12x+62-62+2020=（x-6）2+1984∴当x=6时，（x-6）2的值最小，原式最小值为1984．
例如：分解因式：x2-120x+3456
解：原式=x2-2×60x+602-602+3456=（x-60）2-144=（x-60）2-122=（x-60+12）（x-60-12）=（x-48）（x-72）
（1）分解因式x2-64x+1008；
（2）若y=-x2+6x+1200，求y的最大值；
（3）当m,n为何值时，代数式9m2+8n2+12mn-24n+45有最小值，并求出这个最小值．
共享时间:2022-05-18 难度:2 相似度:1.2
解析 纠错 收藏 下载 组卷 白板
173234. （2024•西光中学•七上二月） 已知A=2x2+3xy-2x-1，B=-x2+xy-1；
（1）求3A+6B；
（2）若3A+6B的值与x无关，求y的值．
共享时间:2024-12-24 难度:1 相似度:1.2
解析 纠错 收藏 下载 组卷 白板
180119. （2024•长安区•七下二月） 化简2（a2b+ab2）-2（a2b-1）-2ab2-2ab.
共享时间:2024-06-13 难度:1 相似度:1.2
解析 纠错 收藏 下载 组卷 白板
175468. （2024•理工大附中•七上二月） 化简：5a2-[4ab-2（a2-3b2）+3（ab-4b2）]．
共享时间:2024-12-22 难度:1 相似度:1.2
解析 纠错 收藏 下载 组卷 白板
179427. （2024•高新一中•七上期中） 已知A=x2+2xy-3y2，B=2x2-2xy-y2．
（1）求A+B；
（2）如果3A-2B+C=0，那么C的表达式是什么？
共享时间:2024-11-26 难度:1 相似度:1.2
解析 纠错 收藏 下载 组卷 白板
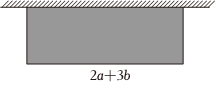173236. （2024•西光中学•七上二月） 德优题库如图，学校要利用专款建一长方形的电动车停车场，其他三面用护栏围起，其中长方形停车场的长为（2a+3b）米，宽比长少（a-b）米．
（1）用a、b表示长方形停车场的宽；
（2）求护栏的总长度；
（3）若a=30，b=10，每米护栏造价100元，求建此停车场所需的费用．
共享时间:2024-12-24 难度:3 相似度:1.07
解析 纠错 收藏 下载 组卷 白板
185197. （2025•西工大附中•七下期中） 先化简，再求值：[（x+2y）2-（5x+y）（5x-y）-5y2]÷（-2x），其中x、y满足x2+y2-2x+6y+10=0．
共享时间:2025-05-14 难度:3 相似度:1.07
解析 纠错 收藏 下载 组卷 白板
173955. （2024•西工大附中•七上一月） 德优题库已知有理数a、b满足|a-6|+|b+5|=0．
（1）a=       ，b=       ，求b-a-2024的值；
（2）如图，在一个无盖正方体展开图中，相对的两个面的数字互为相反数，求x-y+2024的值．
共享时间:2024-10-13 难度:2 相似度:0.7
解析 纠错 收藏 下载 组卷 白板
175475. （2024•理工大附中•七上二月） 某商场销售一种西装和领带，西装每套定价500元，领带每条定价60元．“国庆节”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案．方案一：买一套西装送一条领带；方案二：西装和领带都按定价的90%付款．现某客户要到该商场购买西装20套，领带x条（x＞20）．
（1）若该客户按方案一购买，需付款        元．（用含x的代数式表示）若该客户按方案二购买，需付款        元．（用含x的代数式表示）
（2）若x=30，通过计算说明此时按哪种方案购买较为合算？
共享时间:2024-12-22 难度:2 相似度:0.7
解析 纠错 收藏 下载 组卷 白板
179730. （2024•滨河中学•八上期中） 计算：
（1）（﹣8）﹣（﹣15）+（﹣9）﹣（﹣12）；
 （2）；
（3）x2﹣5xy+xy﹣2x2；
（4）．
共享时间:2024-11-23 难度:2 相似度:0.7
解析 纠错 收藏 下载 组卷 白板

hbh@dyw.com

2025-05-12

初中数学 | 七年级下 | 解答题

  • 下载量
  • 浏览量
  • 收益额
  • 0
  • 14
  • 0
相同试题
试题下载
试题内容
调用试题名称
共享人
唐老师
试题题型
解答题
试题难度
试题题源
2020*西工大*期末
下载次数
168次
下载金币
5德优币（当前结余18德优币）
温馨提示
该试题下载至自主题库后，下载、备课永久免费！
试卷设置
试卷名称
省市校区
阶段科目
年份卷型
选择类型
已选考点
在线训练
是 否
视频讲解
温馨提示
视频讲解正在加载中、请等待！
温馨提示
对不起！这是别人共享的试题，需要下载到自主题库后，可将该试题添加到白板
视频解析购买
支付方式
德优币数
本次消耗0德优币
温馨提示

客服电话：400-816-0029，服务邮箱：610066832@qq.com

视频资源

试题找茬
纠错类型
纠错描述
温馨提示
共享试题、试卷经平台审核通过后方可展示，并永久享用用户下载分红权！