服务热线
搜题▪组卷
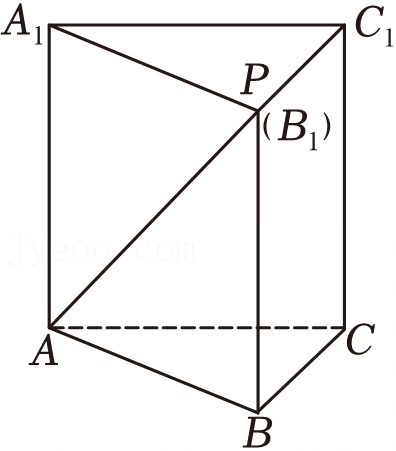
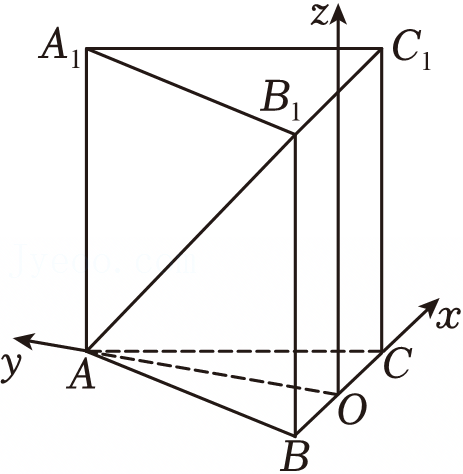
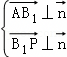 ,所以
,所以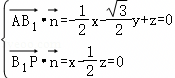 ,
,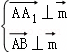 ,所以
,所以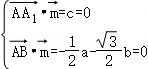 ,
,
A.MN⊥AD
B.平面AND⊥平面ABC
C.三棱锥A﹣BCD的体积为![]()
D.三棱锥A﹣BCD的外接球的表面积为11π
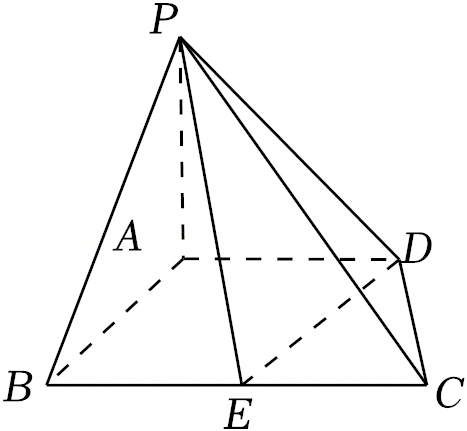
A.l∥BC
C.AB⊥PC
B.平面PDE⊥平面PAD
D.l被球O截得的弦长为1
A.四边形B'EDF是菱形
B.直线A'C与DE所成的角的余弦值是![]()
C.直线AD与平面B'EDF所成角的正弦值是![]()
D..平面B'EDF与平面ABCD所成角的正弦值是![]()
A.点M(3,2,1)关于平面yOz对称的点的坐标是(﹣3,2,﹣1)
B.若直线l的方向向量为![]() =(1,﹣1,2),平面α的法向量为
=(1,﹣1,2),平面α的法向量为![]() ,则l⊥α
,则l⊥α
C.若直线l的方向向量与平面α的法向量的夹角为120°,则直线l与平面α所成的角为30°
D.已知O为空间任意一点,A,B,C,P四点共面,且任意三点不共线,若![]() ,则
,则![]()
A.1个
C..0个
B.无数个
D..1个或无数个
A.直线AC与DB所成的角为120°
B.直线AD与平面ABC所成角的正弦值为![]()
C.平面ABC与平面ABD夹角的余弦值为![]()
D.若E,F分别是AB,CD上的动点,则EF的最小值为![]()
A..两条不重合直线l1,l2的方向向量分别是![]() ,则l1∥l2
,则l1∥l2
B.直线l的方向向量![]() ,平面α的法向量
,平面α的法向量![]() ,则l⊥α
,则l⊥α
C.两个不同的平面α,β的法向量分别是![]() ,则α⊥β
,则α⊥β
D.直线l的方向向量![]() ,平面α的法向量
,平面α的法向量![]() ,则直线l与平面α所成角的大小为
,则直线l与平面α所成角的大小为![]()
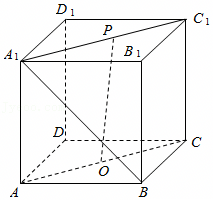
A.三棱锥A﹣D1PD的体积不变
B.A1P∥平面ACD1
C..平面PDB1⊥平面ACD1
D..AP⊥D1C

dvs@dyw.com
2024-11-25
高中数学 | 高二上 | 选择题