微信扫码立即登录

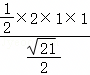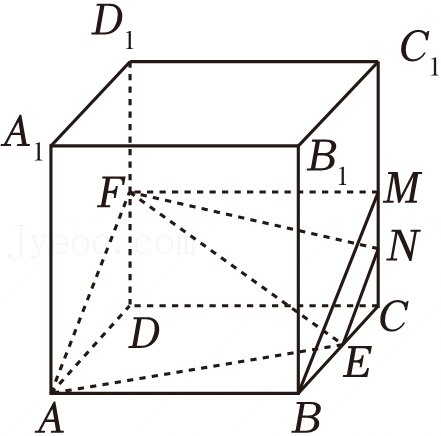
A.．三棱锥B﹣A₁B₁P的体积为定值

B.．当点P在棱DD₁上，AP+PC₁的最小值为  

C.．当点P在正方形CDD₁C₁内，若B₁P与平面CDD₁C₁所成的角为45°，则点P的轨迹长度为π  

D.当点P在棱C₁D₁（不含顶点）上，平面A₁PB截此正方体所得的截面为梯形

A.  

B.数列{y_n}的通项为

C.当n＞3时，   

D.

A.三个平面最多可以把空间分成8部分

B.若直线a⊂平面α，直线b⊂平面β，则“a与b相交”的充要条件是“α与β相交”

C.若α∩β＝l，直线a⊂平面α，直线b⊂平面β，且a∩b＝P，则P∈l   

D.若n条直线中任意两条共面，则它们共面

A.存在唯一点P，使得D₁P⊥B₁C   

B.当点P在AC上移动时，直线D₁P与直线B₁D所成角不变

C.直线D₁P与平面ABCD所成角的最小值为  

D.．当D₁P＝3时，点P的轨迹为圆的一部分

A.．曲线C关于y轴对称

B.|PF₁|+|PF₂|的最小值为

C.△F₁PF₂面积的最大值为  

D.．|OP|的取值范围为

A.．三棱锥Q﹣C₁BD的体积为定值 

B.当点Q为B₁D₁中点时，直线QA₁与平面A₁BD所成角的正弦值为   

C.．当点Q与D₁重合时，三棱锥Q﹣A₁BD的外接球的体积为4

D.．过点Q平行于平面C₁BD的平面被正方体ABCD﹣A₁B₁C₁D₁截得的多边形的面积为2

A.当|MN|最大时，MN与BC所成的角为 

B.三棱锥A₁﹣BNC₁的体积为定值

C.若|DN|＝2，则点N的轨迹长度为2π

D.若N∈平面A₁BCD₁，则BN+NC₁的最小值为

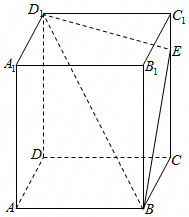
A.．四棱锥B₁﹣BED₁F的体积恒为定值 

B.．存在点E，使得B₁D⊥平面BD₁E

C.对于棱CC₁上任意一点E，在棱AD上均有相应的点G，使得CG∥平面EBD₁

D.存在唯一的点E，使得截面四边形BED₁F的周长取得最小值

A.三棱锥A₁﹣EFG的体积为定值   

B.不存在点G，使得B₁D⊥平面EFG

C.设直线FG与平面BCC₁B₁所成角为θ，则cosθ的最大值为   

D.点F到直线EG距离的最小值为