已知二次函数过坐标原点有且在上的值域为求函数的解析式求解关于的不等式其中为实数

首页 > 试题列表 > 单题解析

166235. （2024•师大附中•高一上二月）已知二次函数f（x）过坐标原点，有f（﹣1）＝f（3），且f（x）在R上的值域为（﹣∞，1]．
（1）求函数f（x）的解析式；
（2）求解关于x的不等式2a﹣ax＞f（x），其中a为实数．

共享时间:2024-12-16 难度:3

纠错

下载

相似

组卷

[考点]

二次函数的值域，解一元二次不等式，函数解析式的求解及常用方法，

[答案]

（1）f（x）＝﹣（x﹣1）²+1；

（2）答案见解析．

[解析]

解：（1）由f（﹣1）＝f（3），
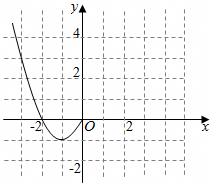
得二次函数f（x）的图象为对称轴为x＝1的抛物线，
又f（x）在R上的值域为（﹣∞，1]，
∴二次函数的图象为开口向下的抛物线，且顶点纵坐标为1，
由此设f（x）＝a（x﹣1）²+1，且a＜0，
已知二次函数f（x）的图象过坐标原点，可得a（0﹣1）²+1＝0，
解得a＝﹣1，则f（x）＝﹣（x﹣1）²+1＝﹣x²+2x；
（2）又2a﹣ax＞f（x），得2a﹣ax＞﹣x²+2x，即（x﹣2）（x﹣a）＞0，
当a＞2时，解得x＞a或x＜2，
当a＝2时，解得x≠2，
当a＜2时，解得x＜a或x＞2．
∴当a＞2时，不等式2a﹣ax＞f（x）的解集为{x|x＞a或x＜2}，
当a＝2时，不等式2a﹣ax＞f（x）的解集为{x|x≠2}，
当a＜2时，不等式2a﹣ax＞f（x）的解集为{x|x＞2或x＜a}．

[点评]

本题考查了"二次函数的值域，解一元二次不等式，函数解析式的求解及常用方法，"，属于"难典题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

138407. （2024•铁一中学•高一上一月）（1）已知关于x的不等式ax²﹣（a+1）x+1＜0的解集为

，求实数a的值；
（2）若a∈R，求关于x的不等式ax²﹣（a+1）x+1＜0的解集．

共享时间:2024-10-26 难度:1 相似度:1.33

解析

纠错

下载

组卷

170234. （2023•西安三中•高二下期末）定义在（﹣1，1）上的函数f（x）和g（x），满足f（x）+g（﹣x）＝0，且

，其中a＞1．
（1）若

，求f（x）的解析式；
（2）若不等式f（x）＞1的解集为

，求m﹣a的值．

共享时间:2023-07-07 难度:1 相似度:1.33

解析

纠错

下载

组卷

171200. （2024•西安八十九中•高一上期中）某学校为了支持生物课程基地研究植物生长，计划利用学校空地建造一间室内面积为900m²的矩形温室，在温室内划出三块全等的矩形区域，分别种植三种植物，相邻矩形区域之间间隔1m，三块矩形区域的前、后与内墙各保留1m宽的通道，左、右两块矩形区域分别与相邻的左右内墙保留3m宽的通道，如图．设矩形温室的室内长为x（m），三块种植植物的矩形区域的总面积为S（m²）．
（1）求S关于x的函数关系式；
（2）求S的最大值，及此时长x的值．

共享时间:2024-11-19 难度:1 相似度:1.33

解析

纠错

下载

组卷

171085. （2024•碑林区•高一上期中）函数f（x）＝ax²+bx+2，a，b∈R．
（1）若f（x）＞0的解集是{x|x＜1或x＞2}，求实数a，b的值及函数f（x）在[1，5]上的最值；
（2）若f（2）＝4，求f（x）＜﹣2x+8的解集（用a表示）．

共享时间:2024-11-15 难度:1 相似度:1.33

解析

纠错

下载

组卷

170347. （2022•长安区一中•高一上期末）函数f（x）＝x²﹣2x﹣2．
（1）当x∈[﹣2，2]时，求函数f（x）的值域；
（2）当x∈[t，t+1]时，求函数f（x）的最小值g（t）．

共享时间:2022-02-23 难度:1 相似度:1.33

解析

纠错

下载

组卷

172068. （2022•铁一中学•高一上期中）某质点在30s内运动速度v是时间t的函数，它的图象如图，用解析法表示出这个函数，并求出9s时质点的速度．

共享时间:2022-11-18 难度:1 相似度:1.33

解析

纠错

下载

组卷

166776. （2024•西安工业大学附中•高一上一月）已知关于x的不等式mx²﹣（3m²﹣m+2）x+6m﹣2≥0．
（1）当m＝2时，求关于x的不等式的解集；
（2）当m＞0时，求关于x的不等式的解集．

共享时间:2024-10-28 难度:1 相似度:1.33

解析

纠错

下载

组卷

166547. （2024•华清中学•高一上一月）已知关于x的不等式2x²+x＞2ax+a（a∈R）．
（1）若a＝1，求不等式的解集；
（2）解关于x的不等式．

共享时间:2024-10-19 难度:1 相似度:1.33

解析

纠错

下载

组卷

166819. （2024•西安八十五中•高一上一月）设函数f（x）＝ax²+（1﹣a）x+a﹣2．若a∈R，解关于x的不等式f（x）＜a﹣1．

共享时间:2024-10-22 难度:1 相似度:1.33

解析

纠错

下载

组卷

171697. （2023•西安八十五中•高一上期中）已知函数f（x）是定义在R上的偶函数，且当x≤0时，f（x）＝x²+2x．
（1）现已画出函数f（x）在y轴左侧的图象，如图所示，请补出完整函数f（x）的图象，并根据图象写出函数f（x）的增区间；
（2）写出函数f（x）的解析式和值域．

共享时间:2023-11-22 难度:2 相似度:0.83

解析

纠错

下载

组卷

171306. （2024•西安中学•高一上期中）已知f（x）是二次函数，且满足f（0）＝2，f（x+2）﹣f（x）＝2x+4．
（1）求f（x）的解析式；
（2）当x∈[m，m+1]，其中m∈R，求f（x）的最小值．

共享时间:2024-11-16 难度:2 相似度:0.83

解析

纠错

下载

组卷

171305. （2024•西安中学•高一上期中）已知y＝f（x）是定义在R上的奇函数，且x＜0时，f（x）＝2^x+1．
（1）求函数f（x）的解析式；
（2）画出函数f（x）的图象，并写出函数y＝f（x）的单调区间及值域．

共享时间:2024-11-16 难度:2 相似度:0.83

解析

纠错

下载

组卷

166998. （2023•西安中学•高一上一月）（1）已知a，b，∈R⁺，证明不等式

（2）解关于x的不等式ax²﹣2（a+1）x+4＞0（a∈R）．

共享时间:2023-10-14 难度:2 相似度:0.83

解析

纠错

下载

组卷

166995. （2023•西安中学•高一上一月）设全集是实数集R，A＝{x|2x²﹣7x+3≤0}，B＝{x|x²+a＜0}．
（1）当a＝﹣4时，求A∩B，A∪B，（∁_RA）∩（∁_RB）；
（2）若B⊆∁_RA，求实数a的取值范围．

共享时间:2023-10-14 难度:2 相似度:0.83

解析

纠错

下载

组卷

166817. （2024•西安八十五中•高一上一月）已知集合A＝{x|（x+2）（x﹣1）＜0}，B＝{x|2x²+（m﹣2）x﹣m＜0}．
（1）当m＝1时，求A∪B；
（2）已知“x∈A”是“x∈B”的必要条件，求实数m的取值范围．

共享时间:2024-10-22 难度:2 相似度:0.83

解析

纠错

下载

组卷

dygzsxyn

2024-12-16

高中数学 | 高一上 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2024-2025学年陕西师大附中高一（上）月考数学试卷（12月份）

更新:2024-12-16 04:45浏览量:15

微信扫码立即登录

AI助手

普通登录

手机登录

微信扫码立即登录

AI助手