首页 > 试卷详情

德优网2024陕西省西安市长安区初中数学考试月考七年级下

2023-2024学年陕西省西安市长安区七年级（下）月考数学试卷（4月份）

试卷总分:120分命题人:dyczsxyn 考试时长:120分钟

一、选择题(8小题共24分)

1. （本题3分）计算x•x²的结果是（　　）

A.3x

B.x²

C.x

D.x³

解析

纠错

下载

相似

组卷

2. （本题3分）下列计算结果正确的是（　　）

A.	B.（a³）⁴＝a⁷
C.（﹣2x）³＝﹣8x³	D.a¹⁰÷a⁵＝a²

解析

纠错

下载

相似

组卷

3. （本题3分）雪花是一种晶体，结构随温度的变化而变化，又名未央花和六出．单个雪花的重量很轻，只有0.00003kg左右，数据0.00003用科学记数法可以表示为（　　）

A.0.3×10^-4

B.0.3×10^-5

C.3×10^-5

D.3×10^-4

解析

纠错

下载

相似

组卷

4. （本题3分）若（x+2）（x-3）=x²+px+q,则p的值为（　　）

A.-5

B.-1

C.5

D.1

解析

纠错

下载

相似

组卷

5. （本题3分）若（n-m）与一个多项式的乘积可以利用平方差公式计算，则这个多项式可以是（　　）

A.m-n

B.m+n

C.mn-1

D.n-m

解析

纠错

下载

相似

组卷

6. （本题3分）若4x²-20x+____=（2x___）²，则横线上分别应填（　　）

A.5²、-5

B.5²、+5

C.10²、+10

D.10²、-10

解析

纠错

下载

相似

组卷

7. （本题3分）张芳家有一个圆柱形的塑料桶，体积是3πx³+6πx²，底面半径为x,则这个塑料桶的高为（　　）

A.3x+6

B.3πx+6

C.3πx²+6πx

D.3πx+6π

解析

纠错

下载

相似

组卷

8. （本题3分）我国南宋数学家杨辉所著的《详解九章算术》一书中，用如图的三角形解释二项和的乘方规律，即（a+b）ⁿ（n=0，1，2，3，…）展开式系数的规律：
$德优题库$
以上系数三角表称为“杨辉三角”，根据上述规律，（a+b）⁶展开式的系数和是（　　）

A.32

B.64

C.128

D.256

解析

纠错

下载

相似

组卷

二、填空题(5小题共15分)

9. （本题3分）若m³•m^x=m⁷，则x= ．

解析

纠错

下载

相似

组卷

10. （本题3分）计算：（3a⁶b³-6ab⁵）÷（-3ab³）= ．

解析

纠错

下载

相似

组卷

11. （本题3分）若a^m=5，aⁿ=3，则a^2m+n的值为．

解析

纠错

下载

相似

组卷

12. （本题3分）已知m²-n²=3，则（m+n）²（m-n）²= ．

解析

纠错

下载

相似

组卷

13. （本题3分） $德优题库$ 如图，点M是AB的中点，点P在MB上．分别以AP，PB为边，作正方形APCD和正方形PBEF，连接MD和ME．设AP=a,BP=b,且a+b=10，ab=20．则图中阴影部分的面积为．

解析

纠错

下载

相似

组卷

三、解答题(13小题共81分)

14. （本题5分）计算：（-3a⁴）²-a•a³•a⁴-a¹⁰÷a²

解析

纠错

下载

相似

组卷

15. （本题5分）计算：（﹣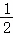

x²y）³•（﹣3xy²）²．

解析

纠错

下载

相似

组卷

16. （本题5分）计算：（-1+2a）（-1-2a）．

解析

纠错

下载

相似

组卷

17. （本题5分）某高分子聚合材料的性能优于铝合金材料，密度为9×10²kg/m³．又知铝合金的密度约为2.7×10³kg/m³，求铝合金的密度是这种材料密度的多少倍．

解析

纠错

下载

相似

组卷

18. （本题5分）先化简，再求值：x（x﹣4y）+（2x+y）（2x﹣y）﹣（2x﹣y）²，其中x＝﹣2，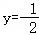

．

解析

纠错

下载

相似

组卷

19. （本题5分）计算：999.8×1000.2（用简便方法计算）．

解析

纠错

下载

相似

组卷

20. （本题5分）化简2（a²b+ab²）-2（a²b-1）-2ab²-2ab.

解析

纠错

下载

相似

组卷

21. （本题6分）若5⁹=a,9⁵=b,用a,b表示45⁴⁵的值．

解析

纠错

下载

相似

组卷

22. （本题7分）大明同学在计算一个多项式乘以﹣2a³时，因抄错符号算成了加上﹣2a³，得到的答案是a³﹣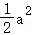

+2，
（1）求这个多项式；
（2）正确的结果应该是多少？

解析

纠错

下载

相似

组卷

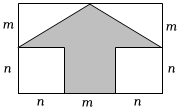23. （本题7分） $德优题库$ 如图是某学校大门口指示牌．已知该指示牌长为（m+2n）cm,宽为（m+n）cm.根据图中所标数据，解决下列问题：
（1）空白部分的面积为 cm²，箭头的面积为 cm²；
（2）当m=10，n=20时，请计算箭头的面积．

解析

纠错

下载

相似

组卷

24. （本题8分）已知A=（2x+y）²-（x-2y）（4x+y），B=（2x²y+5xy²）÷xy-y（11x+3y）．
（1）求A和B；
（2）若x,y满足A+B=3，求4^x•32^y的值．

解析

纠错

下载

相似

组卷

25. （本题8分）已知关于x的代数式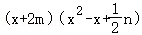

中不含x项与x²项．
（1）求m，n的值；
（2）求代数式m²⁰²³n²⁰²⁴的值．

解析

纠错

下载

相似

组卷

26. （本题10分） $德优题库$ 问题背景
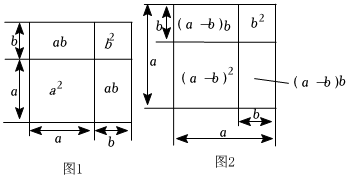
如图，图1，图2分别是边长为（a+b），a的正方形，由图1易得（a+b）²=a²+2ab+b²．
类比探究
类比由图1易得公式（a+b）²=a²+2ab+b²的方法，依据图2中的已知条件推导出完全平方的另一个公式．
解决问题
（1）计算：（2m-n）²= ；
（2）运用完全平方公式计算：105²；
（3）已知（x+y）²=12，xy=2，求（x-y）²的值．

解析

纠错

下载

相似

组卷

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

dyczsxyn

2024-06-13

初中数学 | 考试 | 难度:1.42

下载量
浏览量
收益额

下载试卷	收藏
平行组卷	细目重组
试卷分析	加入白板
加卷篮	更多功能

同类试卷 更多>>

2021届陕西省西安市铁一中学八上数学第一次月考试卷

更新:2020-10-13 01:00浏览量:1135

2022届陕西省西安市师大附中九上数学第一次月考试卷

更新:2021-10-15 06:59浏览量:1038

2020-2021学年陕西省西安市铁一中学八上数学第二次月考试卷

更新:2021-12-15 07:40浏览量:1100

2020-2021学年陕西省西安市西工大附中八上数学第二次月考试卷

更新:2021-01-09 06:11浏览量:786

2023-2024学年陕西省西安市雁塔区高新一中七年级（上）第二次月考数学试卷

更新:2023-12-16 05:47浏览量:476

2023-2024学年陕西省西安市爱知中学八年级（上）第一次月考数学试卷

更新:2023-10-18 05:48浏览量:584

2023-2024学年陕西省西安交大附中航天学校九年级（上）第二次月考数学试卷

更新:2023-10-10 05:49浏览量:478

2023-2024学年陕西省西安市汇知中学七下第一次月考数学试卷

更新:2024-04-25 07:12浏览量:572

2024-2025学年陕西师大附中七年级（上）月考数学试卷（10月份）

更新:2024-10-22 01:41浏览量:70

2024-2025学年陕西师大附中陆港初级中学九年级（上）第一次月考数学试卷（B卷）

更新:2024-10-27 02:08浏览量:60

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

微信扫码立即登录

AI助手

2023-2024学年陕西省西安市长安区七年级（下）月考数学试卷（4月份）

普通登录

手机登录

微信扫码立即登录

AI助手

2023-2024学年陕西省西安市长安区七年级（下）月考数学试卷（4月份）