服务热线
搜题▪组卷
，则
＝ ．
．
＝
，
＝
，
＝
，
＝
或
＝
（不符合题意，舍去），
＝
＝
，
．
的值为 ．
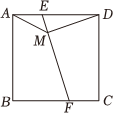
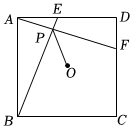如图．在边长为6的正方形ABCD中，点E、F分别在AD、CD上，AE=DF=2，AF、BE相交于点P，O是正方形ABCD的中心，连接OP，则OP的长度为 ．
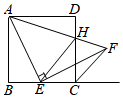
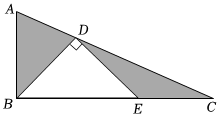如图，在一块直角三角形铁皮ABC中，计划截取一个等腰直角三角形BDE，点D，E分别在AC，BC边上，已知∠ABC=90°，且AB=5，DC=6，EC=2，则剩余阴影部分的面积之和为 ．
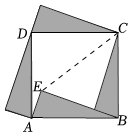清代数学家梅文鼎在《勾股举隅》一书中，用四个全等的直角三角形拼出正方形ABCD的方法证明了勾股定理（如图）．连结CE，若CE=5，BE=4，则正方形ABCD的边长为 ．
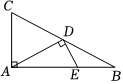
“赵爽弦图”巧妙的利用面积关系证明了勾股定理．如图所示的“赵爽弦图”，△ABH，△BCG，△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，若AB=10，EF=2，则AH= ．
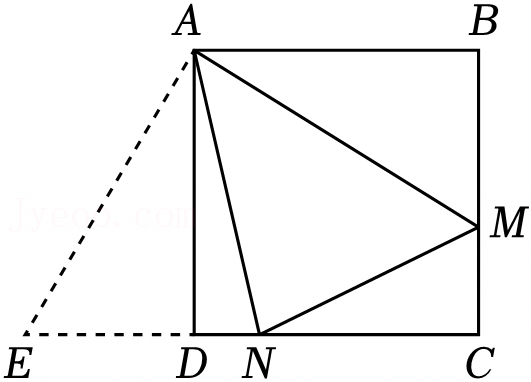
如图，点E、F为正方形ABCD的AD、BC边上两个动点，且AB=8，BF=2AE，连接EF，过点D作DM⊥EF，垂足为M，连接AM，则△ADM面积的最大值为 ．
如图，在△ABC中，AB=AC=4，∠BAC=120°，点D为AC上一点，且满足CD=2AD，E为BD上一点，∠AEB=60°，延长AE交BC于F，则FC的长是 ．
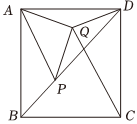如图，四边形ABCD是边长为5的正方形，点P是BD上一动点，以AP为斜边在AP边的右侧作等腰Rt△APQ，∠AQP=90°，连接DQ，CQ．则DQ最小值为 ．
时，则∠BAM＝22.5°；②∠AND+∠MNC＝90°；③若如图位置测得DN＝3，BM＝5，则△ABM的面积为40；④△MNC的周长不变，其中正确结论的序号是 ．
csyn@dyw.com
2024-03-05
初中数学 | | 填空题
纠错
收藏
下载
相似
组卷
解析
如图，CD是等边△ABC边AB上的中线，AC的垂直平分线交AC于点E，交CD于点F，若DF=1，则CD的长为 ．
如图，D是AB延长线上一点，DF交AC于点E，AD∥FC，AE=CE．若AB=5，CF=8，则BD的长是 ．
