服务热线
搜题▪组卷
 AC•BG,AC=4,
AC•BG,AC=4, ×4BG=2BG,
×4BG=2BG,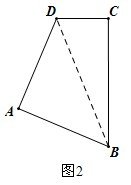
 AD2+
AD2+ CD•BC=25,
CD•BC=25, AD2,S△CBD=
AD2,S△CBD= CD•BC,
CD•BC, AD2+
AD2+ CD•BC=25,
CD•BC=25,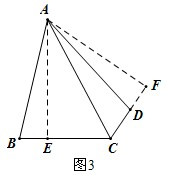
 AE•CE=mn,
AE•CE=mn, (m2+n2),
(m2+n2),
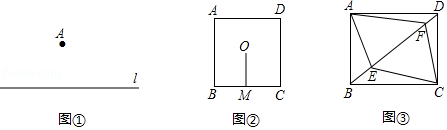
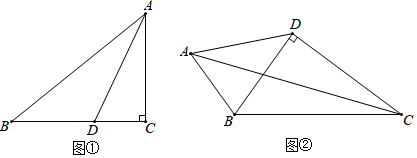

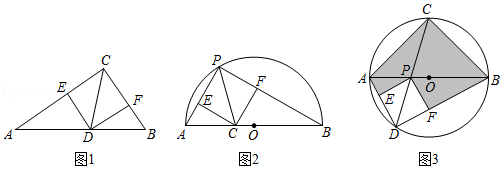

rorsczsx
2022-05-18
初中数学 | 八年级下 | 解答题